Pourquoi ne pas confier au hasard ce qui est trop compliqué à estimer ?
L’union fait la force de la précision
Eh, les gars : quelle heure est-il ? 21h03 ! 21h09 ! 22h17 ! Bon, clairement, il y a un ahuri qui est resté à l’heure d’été, avec une montre qui avance. Mais les deux autres doivent être dans le vrai, à quelques minutes près.

© Photo : Pier-Hugues Pellerin
Bon. Comment faire pour avoir l’heure exacte ? Si je prends la moyenne des deux : [21h03 + 21h09] / 2 = 21h06, c’est ce qui va me donner le résultat le moins mauvais. Ah oui, mais les heures en caractère gras proviennent de montres numériques (dont la précision est d’une minute, sans bavure), alors que celle en italique provient d’une montre à cadran, environ deux fois moins précise (sur le cadran, on lit l’heure à deux minutes près environ). J’ai donc intérêt à croire un peu plus la montre numérique, mais en profitant aussi de la correction que me donne la montre à cadran. Pfff. Ça se complique un peu là. Mais je sais ce que je veux : je veux l’heure h la plus proche possible de 21h03 et 21h09. Donc le résultat qui « minimise la différence », par rapport aux deux. Et en tenant compte du fait que les précisions ne sont pas les mêmes. Cela me donne :
h qui minimise { [h – 21h03] / 1 } + { [h – 21h09] / 2}
On minimise la somme des deux différences pondérées par la précision de chaque mesure. J’ai essayé, 21h04, 21h05, 21h06 : c’est 21h05 qui me donne la meilleure valeur pour le critère ci-dessus : cela fait zéro. Bon, chouette, j’ai réussi à trouver l’heure encore plus précisément… que si j’avais une montre numérique.
Tiens, je vais demander à l’autre ahuri qui se croit encore à l’heure d’été ce qu’il pense de tout ça : il paraît qu’il est informaticien.
J’y crois pas ! Il critique !! Même pas capable de donner l’heure et ça veut donner des leçons !!! Il paraît que je pouvais « résoudre l’équation directement »… Et les ordinateurs, ils ne sont pas là pour ça, des fois ? Oui, il faudrait que l’ordinateur puisse faire la même chose, mais sur des problèmes plus compliqués. Je vais y penser.
Trouver un modèle pour expliquer
Oh, un objet volant ! J’ai vu quelque chose dans le ciel qui clignotait. Quatre fois. J’ai noté les points sur la fenêtre :

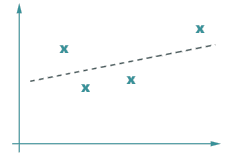
Mais je n’ai pas pu distinguer ce que c’était. Pas assez de lumière. Je vais tracer une ligne pour voir sa trajectoire, mais j’hésite :
 |
 |
| a) une droite ? |
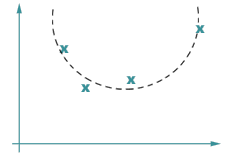
b) un cercle ? |
 |
 |
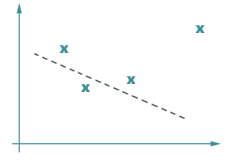
| c) une droite et un point ? | d) un cercle et un point ? |
(a) si je fais passer une ligne droite au mieux par les quatre points, on dirait un avion qui décolle ;
(b) si je fais plutôt passer un cercle, c’est carrément un avion qui fait une cabriole ;
(c) mais il y a aussi le fait que le quatrième point est un peu loin, c’était peut-être autre chose ; un flash Iridium ; comment savoir ? Dans ce dernier cas, si je fais passer une droite par les trois points non douteux, c’est un avion qui… atterrit : vraiment pas pareil ;
(d) et pour compléter, on peut encore supposer que c’est un cercle et un point.
Mmm… il faudrait que je puisse comparer la qualité de mes modèles. Pour trouver le mieux adapté à mes données. Le moins faux, quoi.
Dans ce contexte, un modèle est un objet précis, avec deux aspects :
- Il relie des quantités mesurées à une quantité à estimer, à l’aide d’équations « de mesure ».
- Il définit la structure de la quantité à estimer et la façon dont elle évolue, à l’aide d’équations « de structure » et « d’évolution ».
Les équations définissent la classe de cet objet, son type. Un objet particulier dans cette classe est défini par un vecteur de paramètres : c’est un modèle paramétrique.
Si on cherche par exemple à estimer un cercle, par exemple, il sera défini par son centre et son rayon, et des équations permettront de préciser la courbe que l’on observe dans le plan, ce que l’on mesure, la façon dont le cercle évolue avec le temps, etc.
Oui mais, en fait :
- si c’est une ligne droite, il me faut deux points pour la définir (par deux points passe une et une seule droite) ;
- si c’est un cercle, il me faut trois points pour le définir (par trois points passe un et un seul cercle).
Donc si je n’ai que trois points par exemple, il passe forcément un cercle par ces trois points, comme en (d), donc y faire passer un cercle ne m’apprend rien sur ces points. En revanche, si par ces trois points il passe aussi une ligne droite sans trop d’erreur, alors là, comme en (c), j’ai appris quelque chose : que ces points sont alignés.
Bon, j’ai donc besoin de définir le nombre d de degrés de liberté de mon modèle. C’est le nombre de mesures (mon nombre de points) moins ce qu’il me faut de points pour calculer mon modèle : la dimension du modèle, son nombre de paramètres en fait (deux pour la droite, trois pour le cercle).
Par exemple,
(a) 4 points et une droite à 2 paramètres : d = 4 – 2 = 2
(b) 4 points et un cercle à 3 paramètres : d = 4 – 3 = 1
(c) 3 points et une droite à 2 paramètres : d = 3 – 2 = 1
(d) 3 points et un cercle à 3 paramètres : d = 3 – 3 = 0
Ah bien. Maintenant, je vais faire comme tout à l’heure : regarder ce qui me donne la plus petite erreur. Ici, l’erreur c’est la distance des points à mon modèle : droite ou cercle. Je vais donc estimer le minimum de :
Et le meilleur modèle sera celui qui me donnera la plus petite valeur de ce critère. Tiens : le modèle à zéro degré de liberté, celui qui ne m’apprend rien, sera automatiquement éliminé (si je divise par zéro le résultat est absurde) : c’est parfait.
La distance du point de mesure au modèle, ici, c’est la distance d’un point à une ligne droite ou la distance d’un point à un cercle, j’ai la formule dans un vieux bouquin de math du collège, quand j’étais en 3e, aucun problème. Enfin… sauf que ça fait bien longtemps que je suis plus en 3e ! Mais c’est sûrement pas cet escogriffe d’informaticien qui risque de s’en rendre compte, le benêt.
En fait, ce critère C me permet de faire trois choses en une :
- Estimation : pour des points de mesure donnés et un modèle donné, j’ajuste les paramètres de mon modèle au mieux
- pour minimiser la somme des distances à chaque point ;
- minimiser ce critère me permet de trouver la meilleure estimation.
- Comparaison : pour des points de mesure donnés et tous les modèles, j’ajuste chaque modèle au mieux
- pour choisir le modèle le moins mauvais ;
- minimiser ce critère me permet de deviner quels modèles sont compatibles avec les données.
- Sélection : en écartant un ou des points que je trouve douteux, pour un modèle donné, en ajustant le modèle au mieux, je peux aussi voir si le résultat n’est pas moins mauvais en excluant ces points douteux.
C’est vraiment super. Et j’ai essayé avec mes quatre points : c’est le premier modèle le moins mauvais. Un avion qui décolle, donc : une ligne définie par les quatre points, c’est la solution la moins improbable. Probablement pas de flash Iridium non plus, pour le quatrième point. J’ai même vérifié sur le site web de l’aéroport qui indique, selon le vent, le sens de décollage et d’atterrissage des avions…et je ne me suis pas trompée.
Évidemment, appliquer cette méthode à tous les modèles, ça fait beaucoup d’essais, mais bon, les ordinateurs c’est fait pour ça, hein ? Et puis y’a toujours un ahuri d’informaticien pour les programmer ! Tiens, à propos, ça va lui en boucher un coin à l’abruti d’informaticien de service. Je vais lui expliquer tout ça, tu vas voir s’il va encore me trouver transparente, ce crétin.
Estimer pas à pas la solution à optimiser
Oh comme c’est amusant, qu’il a dit ! Abruti. Que je minimise une distance de Mahanalobis, il a dit (c’est mon critère C, cette distance). Crétin. Il a même ajouté que « dans le cas linéaire, pour un bruit additif Gaussien, j’effectue un test de Fisher », et de un. Gnagnagna. Mais que « si mon modèle était dynamique, variait avec le temps, cela s’apparenterait à un filtre de Kalman », et de deux. Abruti de mes deux, oui (si j’en avais). Upss, excusez-moi, je me suis emportée. Mais tout ça, je le sais aussi.
Sinon, figurez vous qu’un vieux collègue de Môssieur-je-sais-tout avait même concocté le petit logiciel ci-dessous, où on peut sélectionner des points et essayer diverses estimations.
Pour accéder à l’applet Java, autorisez les applets du domaine https://interstices.info. Si votre navigateur n’accepte plus le plug-in Java, mais que Java est installé sur votre ordinateur, vous pouvez télécharger le fichier JNLP, enregistrez-le avant de l’ouvrir avec Java Web Start.
Un spécialiste d’estimation non-linéaire complète mon mécanisme de deux façons.
La distance du point de mesure au modèle est en fait la distance entre le point de mesure et le point du modèle le plus proche du point de mesure comme on le voit sur le schéma ci-dessous :
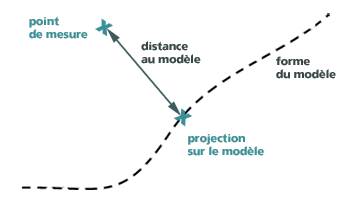
C’est donc la projection (au plus proche) sur le modèle du point de mesure, c’est-à-dire le « point de mesure corrigé ». Ou encore, le point de mesure qui s’adapte parfaitement au modèle.
De plus, pour des raisons mathématiques (une définition plus riche : avec plus de propriétés intéressantes) on prend la distance « au carré » (multipliée par elle-même).
Bien sûr, il faut donc imposer que chaque projection du point de mesure sur le modèle vérifie l’équation du modèle, quelque chose comme :
équation du modèle (projection de la mesure sur le modèle, valeur des paramètres du modèle) = 0
Par ailleurs, pour toutes les inconnues, on choisit en fonction de l’application une estimation initiale, disons une valeur par défaut de la valeur de ces paramètres. Ce nouvel élément est très utile :
- cela permet d’estimer les paramètres du modèle non pas à partir de n’importe quoi, mais de partir d’une valeur de base, à raffiner ;
- s’il y a plusieurs solutions, cela permet de trouver la solution la plus pertinente : celle la plus proche de ce que l’on présupposait a priori ;
- si la solution trouvée est trop différente de la solution initiale, cela permet de la remettre en cause ;
et comme on pondère cette valeur initiale par une précision comme pour les mesures, eh bien, si nous n’avons qu’une très vague idée de la valeur initiale, il suffit de spécifier que la précision est très mauvaise et le terme sera négligé.
Son critère prend donc la forme de :
[distance (projection de la mesure sur le modèle, point de mesure) / précision sur ce point de mesure]2 } / nombre de degrés de liberté
Avec pour chaque point de mesure :
Il estime donc la valeur des paramètres du modèle et chaque projection de la mesure sur le modèle. Et il évalue aussi la précision du résultat à partir de la valeur finale de ce critère.
Pour minimiser le critère :
- (o) il prend comme valeurs initiales
- de la projection de la mesure sur le modèle : le point de mesure lui-même, qui sera donc corrigé
- de la valeur des paramètres du modèle : la valeur initiale des paramètres à améliorer ;
- (i) puis il modifie un peu ces valeurs dans une direction. Si cela minimise le critère tant mieux, si cela a l’effet inverse, il les modifie dans la direction opposée, et le tour est joué. En fait, il calcule localement les meilleures variations des paramètres pour diminuer au mieux le critère ;
- (-) et il recommence jusqu’à ce que le critère soit minimal, donc que la meilleure solution soit trouvée. C’est la meilleure solution locale, c’est-à-dire proche des valeurs initiales, mais en pratique c’est la solution la plus pertinente, ce qui est parfait.
Regardez par exemple l’animation ci-dessous, on y voit comment un critère analogue permet au modèle rouge de la bille d’aller se coller aux mesures bleues :

Cela illustre bien comment on minimise les distances pour arriver à la meilleure estimation.
Tirer au hasard les points pour éliminer ceux qui peuvent gêner
Son petit mécanisme est bien joli, mais il n’est pas aussi malin que le mien ! Moi, non seulement j’estime les paramètres d’un modèle, mais je compare plusieurs modèles, et surtout, je sélectionne les points qui ne sont pas douteux.
Et ça, ce n’est pas facile ! Car si vous avez N points de mesure il y a 2N = 2 x 2… x 2 (N fois) sous-ensembles de mesures à tester, puisqu’il faut faire le choix binaire si oui ou non vous le prenez : 2 possibilités, pour chaque point !!!
Alors, comment faire ? Je connais la méthode la plus maligne, regardez :
- Vous tirez au hasard juste assez de points pour estimer les paramètres (par exemple 2 pour une droite et 3 pour un cercle) et vous minimisez le critère C sans tenir compte du nombre de degrés de liberté ;
- Ensuite, vous regardez la distance de tous les points à votre modèle estimé : les points qui correspondent au modèle sont proches, les points lointains correspondent à un autre modèle (comme l’heure d’été de qui vous savez…), donc vous ne gardez que les points proches en dessous d’une erreur que vous avez choisie ;
- Et vous raffinez l’estimation du modèle avec tous les points proches, pour obtenir la meilleure estimée.
Bien entendu, vous faites recommencer votre ordinateur autant de fois que nécessaire pour que tous les points se trouvent un modèle pour les représenter. Quand il y a le choix entre plusieurs modèles ou plusieurs groupes de points, les meilleurs sont gardés, selon le critère que nous connaissons bien.
Et le tour est joué !!!
L’informaticien bien sûr a des mots compliqués pour dire tout ça : il parle d’« estimation statistique robuste » par une méthode « randomisée ». Ah c’est bien les garçons ça, tiens, de se gargariser de mots compliqués.
En tout cas, ça marche plutôt bien, essayez :
Pour accéder à l’applet Java, autorisez les applets du domaine https://interstices.info. Si votre navigateur n’accepte plus le plug-in Java, mais que Java est installé sur votre ordinateur, vous pouvez télécharger le fichier JNLP, enregistrez-le avant de l’ouvrir avec Java Web Start.
Oh bien sûr, il y a aussi des résultats bizarres, puisque nous avons confié au hasard ce qu’il aurait été bien trop long d’énumérer. Mais il est si facile de ne garder que ce qui colle bien.
Évidemment, s’il n’y a pas assez de points de mesure, ou si les formes qu’ils dessinent sont ambiguës, on obtient des choses inexploitables. Les méthodes industrielles partent de cet algorithme, mais l’adaptent à leur problème pour garantir que le fonctionnement se fera dans de bonnes conditions.
Oh, eh ! Vous n’allez pas vous y mettre vous aussi, hein ? Avec l’autre ahuri qui reste à l’heure d’été, ça suffit bien, merci !! Ce n’est qu’un simple algorithme qui fait déja beaucoup, pas une boîte magique, OK ?
Une méthode « universelle » pour qui en a besoin
Il est tard, la soirée est finie, je suis rentrée avec devinez qui : mon ahuri ! Dans la voiture il avait l’air un peu gêné. C’est timide ces animaux là. Moi je lisais la doc technique de sa voiture. Eh oui, j’aime bien ça. Je lui demande aussi un peu son travail, tout ça, et là il commence à se raconter. Polytechnique, l’envie de faire de la recherche plutôt que de rechercher pouvoir ou argent. Une thèse, le voilà Docteur d’Université, cet ingénieur supérieur. Il a d’ailleurs développé des méthodes d’estimation pour des modèles assez compliqués, mais… basées sur ce que je vous ai raconté.
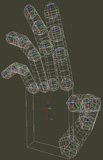
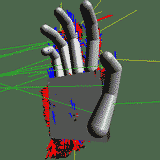
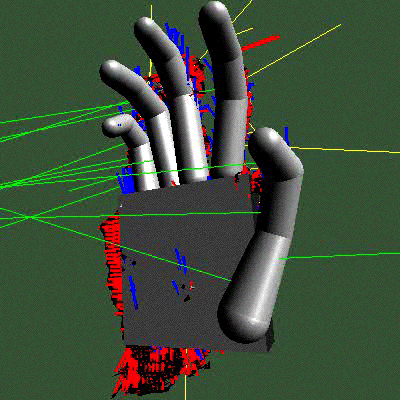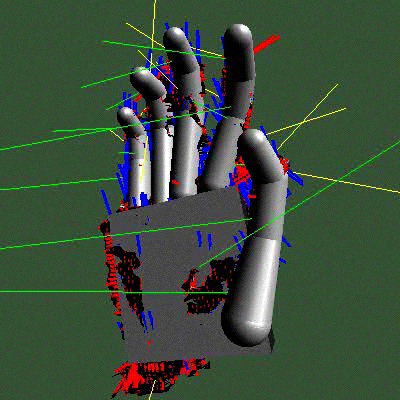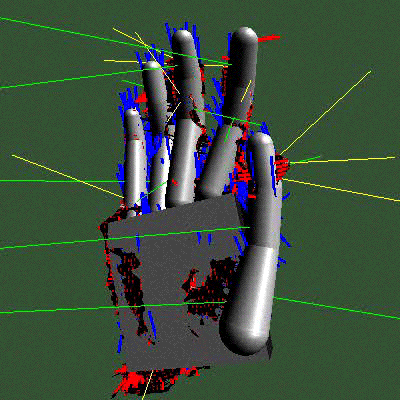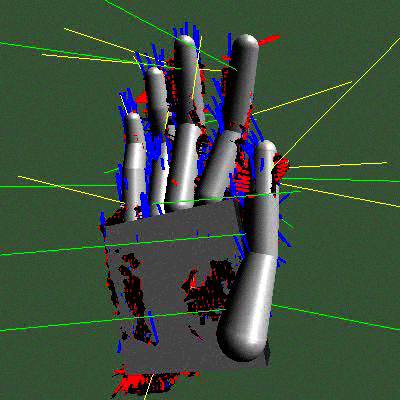
Par exemple, un modèle qui est l’avatar d’une main : on voit le modèle géométrique à gauche, la façon dont on colle le modèle aux données à côté (on voit les traits qui correspondent aux projections pour calculer les distances) et un résultat d’une estimation sur une séquence réelle. Les applications sont multiples, transmission de la langue des signes, nouvelles interfaces homme-machine, etc.
 |
 |
 |

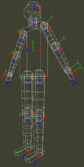
Il l’a aussi appliqué à un avatar de corps humain, pas très détaillé mais suffisant pour analyser dans une séquence vidéo des postures, des gestes, etc. Il est utilisé dans des systèmes de vidéo-surveillance par exemple. Vous découvrez comme précédemment le modèle et le résultat d’une estimation (avec toujours les traits des distances).
 |
 |
 |
 |



Et puis, plus généralement, il a raconté comment il se régalait avec les équations, pour concevoir et développer les logiciels qui y sont liés et aller jusqu’aux applications.
Moi, ça vous étonnera peut-être de la part d’une jeune femme, mais c’est en mécanique que je suis très forte. Mais quand sa voiture est tombée en panne ce soir là, je ne l’ai pas aidé, c’était son problème. Oh, il a fini par trouvé la cause de la panne, le fusible électrique qui avait mystérieusement disparu de son tableau. Il a même fini par trouver où avait glissé ce coquin de fusible. Oui. Il était sur moi. Et je l’avais très très bien caché.
- De la perception du mouvement aux systèmes adaptatifs : une synthèse par Thierry Viéville et Olivier Faugeras, téléchargeable en PDF (400 Ko) ;
- Estimation de modèles paramétrés de mouvement par moindres carrés non-linéaire, R. Mongrain, M. Cyr, M. Bertrand, téléchargeable en PDF (7 Mo) ;
- Implémentation d’une variante de la méthode d’estimation de Kanatani, T. Viéville, D. Lingrand, F. Gaspard ;
- Estimation paramétrique multi-modèle robuste : une introduction, A.C. Belon ;
- Quelques idées sur le concept d’adaptation en vision par ordinateur, Thierry Viéville.
Newsletter
Le responsable de ce traitement est Inria. En saisissant votre adresse mail, vous consentez à recevoir chaque mois une sélection d'articles et à ce que vos données soient collectées et stockées comme décrit dans notre politique de confidentialité
Niveau de lecture
Aidez-nous à évaluer le niveau de lecture de ce document.
Votre choix a été pris en compte. Merci d'avoir estimé le niveau de ce document !
