La géométrie des contacts entre biomolécules
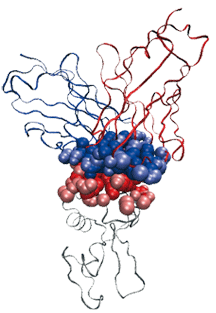
Un complexe antigène (chaîne polypeptidique grise) – anticorps (chaînes polypeptidiques bleu et rouge), et les atomes participants à l’interface. L’objet de cet article est d’expliquer comment décrire cette interface.
Image : F. Cazals
Durant la dernière décennie, la génomique, qui décrypte les séquences des acides nucléiques (ADN, ARN) des différents organismes, et la protéomique, qui étudie l’ensemble des protéines associées, ont bien progressé. En revanche, il reste encore beaucoup à apprendre sur la fonction de ces biomolécules et sur la manière dont elles interagissent selon leur structure spatiale : c’est l’objet de la biologie structurale.
L’étude des rapports entre la structure et la fonction recouvre deux problématiques : la première s’intéresse au repliement, grâce auquel une biomolécule adopte sa structure tridimensionnelle ; la deuxième étudie l’arrimage, c’est-à-dire les processus par lesquels deux ou plusieurs molécules s’associent pour former un complexe.
Expérimentalement, les études structurales se fondent sur la détermination de la structure en trois dimensions des biomolécules, principalement grâce à la cristallographie aux rayons X, à la résonance magnétique nucléaire (RMN) et à la microscopie cryoélectronique (examen à l’aide d’un microscope électronique de fines particules congelées). Les structures ainsi déterminées permettent, à haute résolution, d’examiner l’architecture spatiale à l’échelle atomique. Par exemple, lorsqu’un cristal contient deux protéines formant un complexe, on voit comment des molécules d’eau sont prises en étau entre deux protéines. La première structure haute résolution obtenue à partir d’un cristal a été celle de l’hémoglobine, protéine qui assure le transport de l’oxygène dans le sang. John Kendrew et Max Perutz ont réalisé ce travail en 1960, ce qui leur valut le prix Nobel de chimie en 1962. À ce jour, toutes les structures déterminées sont répertoriées dans une base de données — la Protein Data Bank — accessible à la communauté scientifique.
Outre l’acquisition des données, les études structurales réalisent la modélisation des structures résolues. La modélisation est d’ailleurs la seule façon d’appréhender certains systèmes, comme les protéines membranaires, qui ne cristallisent pas, ou les grosses protéines, auxquelles on ne peut appliquer la RMN. Dans le cadre de la génomique structurale, qui vise à répertorier l’ensemble des interactions possibles entre les protéines codées par le génome, un thème important de la modélisation est l’étude des interactions non covalentes entre deux protéines. En cela, la géométrie et la topologie nous aident. Une fois connues les positions des atomes de deux protéines formant un complexe cristallisé, ainsi que les positions de molécules d’eau piégées dans le cristal, nous cherchons à identifier les atomes participant à l’interface, à décrire la géométrie et la topologie de cette interface, et enfin, à évaluer le rôle des molécules d’eau. Cette modélisation devrait permettre, à terme, de prédire la formation de tels complexes.
Les molécules et leur environnement
Dans les cellules in vivo, les macromolécules sont plongées dans un bain de solvant, d’ions, de métabolites, etc. Elles sont soumises à l’agitation thermique, si bien qu’elles entrent en collision avec les molécules du solvant et s’entrechoquent. Ces rencontres permettent la formation de liaisons faibles, dites liaisons hydrogène : la molécule d’eau, par exemple, présente un faible déséquilibre des charges électriques, légèrement négatives sur l’oxygène, et légèrement positives sur les deux atomes d’hydrogène. Une telle molécule polaire attire à elle d’autres molécules polaires, avec lesquelles elle forme une liaison hydrogène (dix fois plus fragile que la liaison covalente). Les liaisons hydrogène jouent un rôle important en biologie : elles interviennent dans la solvatation des biomolécules, en favorisant la formation de réseaux, et la formation de régions hydrophobes desquelles elles sont exclues.
De façon générale, la description d’un système constitué de biomolécules et de leur solvant fait intervenir son énergie potentielle et son entropie, cette dernière mesurant son état de désordre. Les modèles ont vocation à évaluer ces quantités d’énergie ainsi que leurs variations, notamment lors de la formation d’un complexe protéine-protéine. Nous allons voir comment on en décrit la géométrie.
Chaque molécule vibre à diverses fréquences, les hautes fréquences correspondant aux vibrations au niveau des liaisons chimiques, les basses fréquences à des mouvements d’ensemble de la molécule. L’énergie interne E d’un tel système est composée de son énergie cinétique et de son énergie potentielle. Cette dernière fait intervenir un terme correspondant aux liaisons chimiques et un autre correspondant aux liaisons non covalentes. Celui-ci comprend deux composantes, l’énergie de van der Waals, qui correspond aux interactions entre les dipôles induits par les fluctuations des nuages électroniques autour des noyaux, et l’énergie electrostatique correspondant aux attractions – répulsions entre charges.
En raison de la dynamique évoquée ci-dessus, les propriétés macroscopiques permettant d’appréhender un tel système correspondent à des moyennes. Par exemple, la moyenne U de l’énergie interne E se calcule sur l’ensemble des états possibles du système. Mais pour décrire un tel système, il faut aussi prendre en compte son entropie S qui code son désordre. Pour un système à température T et pression P constantes, la quantité d’intérêt est l’énergie libre de Gibbs définie par G = H – TS, avec l’enthalpie H = U + PV. En particulier, l’énergie G atteint un minimum local aux points d’équilibre du système. De plus, l’étude de l’association entre deux protéines, entre leurs états hors complexe et l’état en complexe, requiert le calcul de la variation d’énergie libre :
ΔG = ΔH – ΔS
D’après la discussion ci-dessus, la variation d’enthalpie ΔH correspond à des changements de l’énergie électrostatique et de l’énergie d’interaction de van der Waals. Quant au terme ΔS, il rend compte du gain ou de la perte de flexibilité des partenaires au niveau de l’interface ainsi que du gain ou de la perte de structure au niveau du solvant.
Diverses méthodes ont été développées pour évaluer l’énergie ΔG, et nombre d’entre elles exploitent des paramètres géométriques décrivant l’interface. Par exemple, la compacité de l’empilement des atomes à l’interface permet de décrire l’énergie d’interaction de van der Waals ; la surface accessible au solvant qui se trouve enfouie lors de la formation du complexe est reliée à l’effet hydrophobe — l’ensemble des mécanismes favorisant la formation de régions hydrophobes —, et permet sous certaines hypothèses d’approximer ΔG ; la fréquence des paires d’atomes voisins à l’interface est corrélée avec la solubilité des résidus, et peut aussi être utilisée pour calculer une approximation de ΔG.
Bien entendu, ces calculs sont approchés. Ils sont en fait d’intérêt majeur dans les études d’arrimage, de façon à identifier des conformations presque natives, entre deux protéines ou une protéine et un ligand. De tels systèmes peuvent ensuite être optimisés, la variation ΔG étant alors calculée avec des méthodes plus précises relevant de la thermodynamique.
En théorie, la modélisation d’assemblages macromoléculaires devrait reposer sur la mécanique quantique qui décrit les interactions à l’échelle des atomes et des particules élémentaires. Hélas, les équations associées ne sont plus solvables au-delà de quelques dizaines d’atomes, alors que les assemblages de biomolécules, tels que les capsides de virus par exemple, comportent jusqu’à plusieurs centaines de milliers d’atomes. Nous utilisons plutôt un modèle de van der Waals, dû au physicien hollandais Johannes Diderik van der Waals (1837-1923), où chaque atome est représenté par une boule dont le rayon dépend de ses propriétés. Une molécule est donc une collection de boules, chacune délimitée par une sphère. On scinde ces boules en deux groupes, celles de la colonne vertébrale de la protéine et celles correspondant aux chaînes latérales des acides aminés, accrochées à la colonne vertébrale.
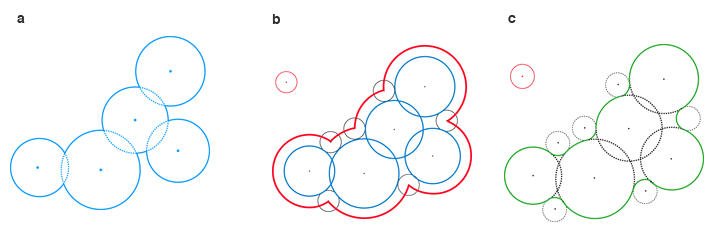
La surface d’une molécule représentée par des boules de van der Waals est constituée par la frontière de l’ensemble de ces boules (a) : c’est la surface de van der Waals. La surface accessible par le solvant est l’ensemble des positions possibles du centre d’une boule représentant le solvant, qui roulerait sur la surface de van der Waals (b). La surface de Connolly prend en compte le recouvrement des creux par la boule représentant le solvant (c).
Infographie : Pour la Science
Dans ce modèle, une molécule – une famille de boules de van der Waals – interagit avec son environnement à travers sa surface moléculaire, dont on donne trois types de représentations. Le bord de l’union des boules de van der Waals, dénommée surface de van der Waals, sert surtout à visualiser la molécule. Pour étudier la solvatation d’une protéine, on a besoin de connaître la surface accessible au solvant. On la déduit de la surface précédente en faisant rouler dessus une boule mimant une molécule d’eau : le centre de cette boule dessine une nouvelle surface, dénommée surface accessible au solvant.
On s’intéresse aussi à la manière dont la boule qui représente le solvant recouvre les creux de la surface de van der Waals : on obtient ainsi la surface de Connolly, troisième type de représentation de la surface moléculaire. Celle-ci est utilisée pour modéliser le champ électrique induit par les atomes chargés, qu’ils appartiennent à la protéine ou au solvant.
Les représentations géométriques
Traditionnellement, on étudie la répartition spatiale d’un nuage de points ou d’objets (ici les atomes des molécules) à l’aide d’un diagramme de Voronoï, qui caractérise les régions d’influence de ces points. Dès 1644, René Descartes a utilisé de tels diagrammes pour montrer la position des astres dans le système solaire et ses environs. Le premier mathématicien à avoir étudié ces diagrammes en deux et trois dimensions fut le mathématicien français Gustav Lejeune-Dirichlet (1805-1859). Enfin, le mathématicien ukrainien Georgii Feodosevich Voronoï (1868-1908) a défini ces diagrammes pour un nombre quelconque de dimensions.
Dans le plan, la région d’influence d’un point donné est un polygone, dont les arêtes sont formées par les médiatrices des segments qui joignent ce point à chacun de ses proches voisins. En trois dimensions, la région associée à un point donné est définie comme l’intersection des demi-espaces bordés par les plans médiateurs qui séparent deux à deux tous les autres points. C’est donc une région convexe, éventuellement non bornée.
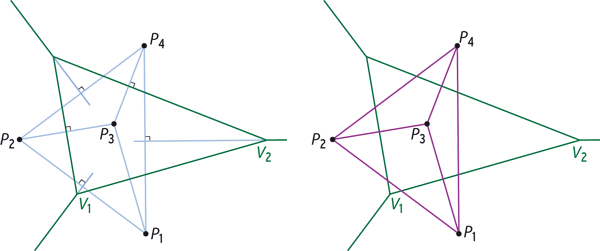
Traitement géométrique d’un ensemble de points P1, P2, P3, et P4 dans le plan. On trace le diagramme de Voronoï à l’aide des médiatrices des segments joignant les points deux à deux : les segments et les médiatrices de construction sont en bleu clair, le diagramme en vert (à gauche). L’ensemble des segments constitue la triangulation de Delaunay (en violet, à droite) : elle contient ici quatre sommets, six arêtes et trois triangles. La triangulation de Delaunay est duale du diagramme de Voronoï, c’est-à-dire qu’elle contient les mêmes informations géométriques : ainsi l’arête de Delaunay P1P3 est duale de l’arête de Voronoï V1V2.
Infographie : Pour la Science
Il est plus aisé d’étudier le dual (ou équivalent géométrique) du diagramme de Voronoï : la triangulation de Delaunay, nommée ainsi d’après les travaux du mathématicien russe Boris Delone (1890-1980), Delaunay étant sa transcription du cyrillique. Voici comment on l’obtient en deux dimensions. Pour chaque point du nuage d’origine, on trace un segment vers le point associé à chacune des régions de Voronoï voisines (comme on l’a fait avant de tracer les médiatrices) : on obtient un ensemble d’arêtes qui pointent toutes vers le point de départ. De même, un triplet de régions de Voronoï voisines définit un triangle.
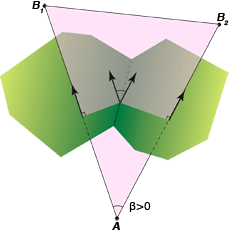
En trois dimensions, un triangle de Delaunay (en violet) est constitué par les centres d’un atome de type A et deux atomes de type B (B1 et B2) ; les arêtes de Delaunay AB1 et AB2 sont duales des facettes de Voronoï (en vert). Ces facettes sont dites connectées, car elles partagent une arête de Voronoï. L’angle dièdre entre les facettes est égal à l’angle entre les arêtes de Delaunay AB1 et AB2. Cet angle β est compté positivement dans ce cas où les deux arêtes AB1 et AB2 impliquent deux atomes de type B, et négativement si les deux arêtes impliquent deux atomes de type A et un atome de type B (A1B et A2B). Cet angle sert à définir ce qu’on appelle une courbure moyenne discrète, donnant des informations sur la spécificité de l’interaction des molécules.
Infographie : Pour la Science
En trois dimensions, la même construction définit des arêtes, des triangles et des tétraèdres. La propriété de dualité du diagramme de Voronoï et de la triangulation de Delaunay signifie que les deux possèdent les mêmes propriétés géométriques. En deux dimensions, une arête de Delaunay est duale d’une arête de Voronoï. En trois dimensions, une arête de Delaunay est duale d’une facette de Voronoï.
On pourrait déterminer le diagramme de Voronoï de l’ensemble des centres des atomes dans le cadre du modèle de van der Waals. Cependant, ce diagramme ne rend pas compte des différences de rayons des atomes. On pondère alors les atomes en fonction de leur rayon, le poids étant défini comme le carré du rayon, et on trace un diagramme, dit de puissance, équivalent au diagramme de Voronoï, en remplaçant la distance euclidienne entre les atomes par une distance corrigée par leur poids. Si les sphères sont toutes de même rayon, le diagramme de puissance est identique au diagramme de Voronoï. Les deux diagrammes étant affines – les cloisons entre les régions appartiennent à des plans –, nous garderons le terme de diagramme de Voronoï dans la suite.
On peut en outre mimer un processus de dilatation ou d’érosion des boules, et les observer à diverses échelles, en ajoutant ou retranchant à leur poids un paramètre, appelons-le α. Quand α est nul, une boule a un poids inchangé ; quand α croît par valeurs positives, la boule se dilate ; si α décroît par valeurs négatives, la boule s’érode. Étant donnée une famille de boules, on définit une famille de sous-ensembles de la triangulation de Delaunay, l’α-complexe.
Pour un α donné, l’α-complexe est construit comme la triangulation de Delaunay, à ceci près que chaque région de Voronoï est remplacée par son intersection avec la boule, dilatée ou érodée, qui lui est associée, définissant la région restreinte. Ainsi, au lieu de considérer une arête entre deux régions de Voronoï voisines, on considère une arête entre deux régions restreintes voisines. De même, trois et quatre régions restreintes voisines définissent respectivement un triangle et un tétraèdre.
L’α-complexe est la construction géométrique de référence pour manipuler les modèles de van der Waals. Ainsi la surface de van der Waals se calcule à partir du 0-complexe des sphères de van der Waals. De façon analogue, la surface accessible au solvant se déduit du 0-complexe des sphères de van der Waals dont le rayon a été augmenté de celui de la molécule d’eau mimant la couche de solvatation. L’α-complexe est aussi la construction de référence pour modéliser les interfaces.
Trois interfaces
La dualité des diagrammes représentés fournit deux vues complémentaires d’une interface. D’une part, les arêtes identifient implicitement les sphères qui définissent les atomes de l’interface ; d’autre part, les facettes de Voronoï, duales de ces arêtes, définissent une surface polyédrique séparant les deux partenaires.
 |
 |
|
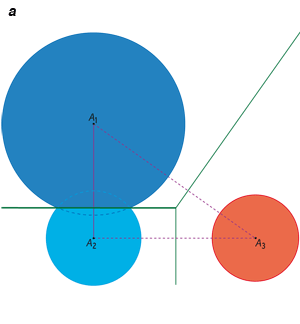
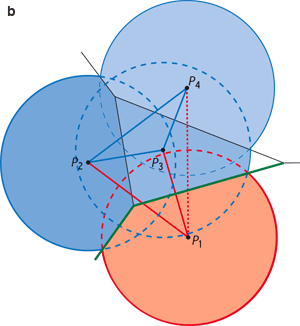
Construction de l’α-complexe en deux dimensions, pour α = 0 et pour trois points A1, A2 et A3 (a). On trace des disques de centres A1, A2 et A3. On restreint ensuite chaque disque à son intersection avec la région de Voronoï de son centre (en couleurs). Lorsque deux ou trois régions restreintes se touchent, l’arête (ou le triangle) qui joint leurs centres appartient au 0-complexe. Le 0-complexe des trois points ne contient ici que l’arête A1A2. Imaginons maintenant que les quatre points P1, P2, P3 et P4 (vu précédemment) soient les centres de disques représentant les atomes de deux molécules, P1 appartenant à une molécule rouge et P2, P3 et P4 à une molécule bleue (b). L’arête P1P4 n’appartient pas au 0-complexe, car les régions restreintes associées aux disques P1 et P4 ne sont pas voisines. Les arêtes du 0-complexe qui joignent des atomes de deux molécules (en rouge) identifient les atomes participant à l’interface, et les facettes de Voronoï duales (en vert) définissent l’interface elle-même. |
|
Le diagramme de Voronoï fournit une définition naturelle de voisinage : deux atomes sont voisins si leurs régions de Voronoï sont voisines, c’est-à-dire partagent une facette de Voronoï. Mais en définissant de tels contacts, il arrive que l’on considère comme voisins deux atomes éloignés. Une définition de voisinage plus adaptée utilise le 0-complexe. Plus précisément, en considérant les boules de van der Waals dont le rayon a été augmenté de celui de la molécule d’eau, on s’intéresse à l’intersection des régions restreintes plutôt qu’à celle des régions de Voronoï (voir la figure ci-dessus). Dans ce cas, les paires d’atomes sélectionnées sont les arêtes du 0-complexe, les longues arêtes étant exclues (puisqu’alors les régions restreintes ne se touchent pas).
Cependant, si l’on veut étudier le rôle des molécules d’eau, la sélection d’arêtes courtes ne suffit pas. Notons A et B les deux molécules formant un complexe et E les molécules d’eau cristallographiques piégées entre les molécules. On définit trois interfaces différentes : l’interface AB entre les deux protéines décrit le contact entre les deux partenaires du complexe ; l’interface AE–BE entre chaque protéine et les molécules d’eau décrit le contact entre les partenaires et le solvant ; l’union ABE des deux types d’interfaces permet d’appréhender leur position relative.
Une question naturelle est de savoir si une interface donnée est morcelée, et pour chaque morceau, s’il contient des trous. Cette question vise à qualifier la topologie de l’interface, et pour y répondre, il faut examiner la façon dont les facettes de Voronoï se recollent. Rappelons que deux facettes de Voronoï sont dites connectées si elles partagent une arête de Voronoï.
Considérons une collection de facettes de Voronoï. S’il existe un chemin entre n’importe quelle paire de facettes de telle sorte que chaque paire de facettes consécutives est connectée, la collection est dite connectée. De plus, si cette collection est maximale – on ne peut ajouter aucune autre facette connectée –, on dit qu’elle définit une composante connexe de l’interface. Une composante connexe correspond donc à un ensemble d’atomes des protéines, tels qu’une région restreinte de l’une a une intersection avec une région restreinte de l’autre, laquelle a une intersection avec une région restreinte de la première, etc.
Nous avons par exemple modélisé un complexe antigène-anticorps AB.
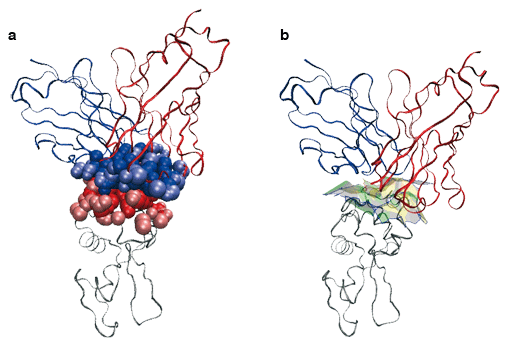
Les chaînes de polypeptides sont représentées comme des rubans. Une enzyme (lysozyme, en gris) est accrochée à un morceau d’anticorps de souris (en rouge et bleu). On modélise les atomes participant à l’interface entre les deux macromolécules par des boules de van der Waals (en a). Pour étudier la géométrie de cette interface, on définit des facettes planes (facettes vertes, jaunes et grises, à droite), chacune étant définie par deux boules de van der Waals dans ce qu’on appelle le diagramme de Voronoï des atomes.
Images : F. Cazals
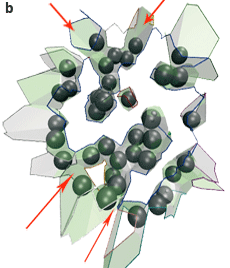
L’interface AB entre les deux protéines contient trois composantes connexes : une grande au centre, et deux petites en haut et en bas (a, ci-dessous). L’interface AE–BE des protéines avec les molécules d’eau cristallographiques contient sept composantes connexes, qui correspondent aux interstices entre les atomes (b, ci-dessous) : ils sont intéressants dans ce cas pour qualifier la spécificité de l’anticorps.
 |
 |
|
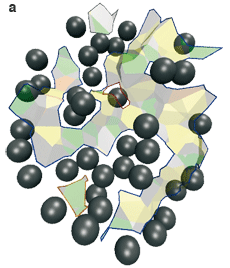
L’interface du complexe anticorps-antigène AB (représentée par les facettes de Voronoï) est morcelée. Les boules grises sont les molécules d’eau (les biomolécules ne sont pas représentées). L’interface directe entre les deux molécules (a) contient trois composantes connexes, c’est-à-dire pour lesquelles il existe un chemin entre facettes de Voronoï connectées : une grande composante connexe est au centre (chemin tracé en bleu), une petite en haut (en gris) et une petite en bas (en rouge). L’interface entre chaque molécule et les molécules d’eau (b) contient sept composantes connexes qui forment des criques entre les deux protéines (les flèches rouges en désignent quatre). |
|
Lorsqu’une facette de l’interface AB et une facette de l’interface AE–BE sont connectées par une arête de Voronoï, on fusionne leurs composantes connexes respectives, qui deviennent une composante connexe de l’interface ABE. Celle-ci est donc définie comme l’union des interfaces AB et AE–BE, et quantifie leur position relative. En particulier, l’interface ABE permet d’appréhender la taille des trous entre les deux partenaires, lesquels sont comblés par les molécules d’eau.
Emboîtement et courbure
Une question centrale concernant une interface est celle de la complémentarité géométrique entre les partenaires. Celle-ci correspond à un emboîtement des bosses dans les creux, comme en a eu l’intuition le chimiste allemand Emil Fischer (1852-1919), lauréat du deuxième prix Nobel de chimie en 1902. Cette propriété peut être quantifiée à l’aide de la notion de courbure.
En mathématiques, la courbure d’une surface lisse s’exprime à l’aide de sphères (dites sphères osculatrices principales) que l’on trace de manière à ce qu’elles épousent au mieux la forme de cette surface. Les inverses des rayons de ces sphères définissent les courbures principales. Le produit de ces courbures est appelé courbure de Gauss, et leur moyenne arithmétique est la courbure moyenne. Deux théorèmes fameux, résultats des recherches du mathématicien allemand Carl Friedrich Gauss (1777-1855), relient la courbure de Gauss à la géométrie de la surface et à sa topologie. Par exemple, l’intégrale de cette courbure sur un ballon de foot ou de rugby vaut 4π.
Pour appréhender la façon dont une surface est plongée dans l’espace ambiant, il faut utiliser la courbure moyenne. Dans notre cas, l’interface AB est une surface polyédrique, pour laquelle on définit une courbure moyenne discrète : la courbure moyenne portée par une arête est égale au produit de sa longueur par son angle dièdre, compté positivement ou négativement selon la nature des atomes que l’arête joint.
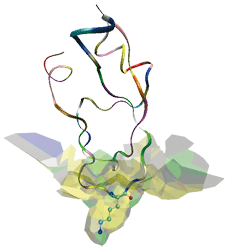
Interface d’un complexe protéase-inhibiteur. La protéase, non représentée, a un site actif en cylindre creux, comparable à une serrure. L’inhibiteur (la trypsine du pancréas) possède la clé susceptible de pénétrer dans la serrure. Il est représenté sous la forme de rubans et sa chaîne latérale Lysine 15, la clé, en mode fil de fer. Le modèle a permis de décrire comment l’inhibiteur s’emboîte dans la protéase et de recenser les atomes impliqués.
Image : F. Cazals
Ceci est illustré pour un complexe protéase-inhibiteur. La protéase est une enzyme qui hydrolyse les protéines, par exemple lors de la digestion. Son site actif est concave et de forme cylindrique : sa courbure moyenne est élevée. L’inhibiteur vient remplir ce site actif (ce qui inhibe sa fonction) par une de ses chaînes latérales : la Lysine 15. Du fait de la position centrale de la Lysine 15 le long de l’axe du cylindre, les atomes de l’inhibiteur ont, en moyenne, environ deux fois plus de voisins que les atomes de la protéase.
Finalement, notre modèle permet de mieux modéliser l’énergie du sytème : il a amélioré nos connaissances sur les complexes de protéines, dont les interfaces étaient modélisées avec des méthodes plus élémentaires. Par exemple, les atomes à l’interface étaient définis comme ceux dont tout ou partie de la surface accessible au solvant se trouvait couverte par le partenaire dans le complexe. Notre modèle montre que 13 pour cent d’atomes supplémentaires sont impliqués à l’interface, ces atomes ne perdant pas de surface accessible au solvant. Ce sont essentiellement des atomes de la colonne vertébrale des protéines, ce qui surprend, car on pensait que ces atomes avaient un rôle plus limité dans les mécanismes d’arrimage.
Autre exemple : les composantes connexes de l’interface AE–BE permettent d’apprécier précisément le rôle des molécules d’eau cristallographiques. Lorsque les molécules d’eau sont incorporées au diagramme de Voronoï, le nombre d’atomes à l’interface augmente en moyenne de 45 pour cent, et la proportion d’atomes enfouis, c’est-à-dire qui ne contribuent pas à la surface accessible au solvant du complexe, passe de 38 à 68 pour cent. Les propriétés d’hydratation des interfaces recèlent encore nombre de mystères et leur étude géométrique permettra d’améliorer la prédiction des interactions.
Quelques références vous sont proposées pour en savoir plus sur la géométrie des biomolécules.
En français
- Intervor, logiciel du modèle présenté dans l’article
- J-D. Boissonnat et M. Yvinec, Géométrie algorithmique, Édiscience International, 1995
En anglais
- F. Cazals, F. Proust, R. Bahadur et J. Janin, Revisiting the voronoi description of protein-protein interfaces, in Protein Science, 2006 (en PDF, 569,99 Ko)
- About protein structure
- Biophysical society online textbook
- O. Smart, An overview of molecular forces in relation to protein structure
- Institut Pasteur, European Molecular Biology Organization (EMBO) course on biomolecular simulation
- The Critical Assessment of PRediction of Interactions (CAPRI), The CAPRI contest
Logiciels/environnements pour la modélisation moléculaire
- Visual Molecular Dynamics (VMD), a molecular visualization program
- PyMOL, a molecular visualization system
- The Python Molecule viewer (PMV), a molecule viewer
Une première version de cet article est parue dans le dossier n°52 La modélisation informatique, exploration du réel de la revue Pour la Science, numéro de juillet/septembre 2006.
Newsletter
Le responsable de ce traitement est Inria. En saisissant votre adresse mail, vous consentez à recevoir chaque mois une sélection d'articles et à ce que vos données soient collectées et stockées comme décrit dans notre politique de confidentialité
Niveau de lecture
Aidez-nous à évaluer le niveau de lecture de ce document.
Votre choix a été pris en compte. Merci d'avoir estimé le niveau de ce document !

Frédéric Cazals