Symétries et morphogenèse
Le terme de morphogenèse est employé de façon très générale pour désigner le processus d’apparition d’une forme. Quels sont les liens entre la morphogenèse et la notion de symétrie ? Voici quelques pistes à explorer.
Qu’est-ce qu’une symétrie ?
La définition mathématique d’une symétrie, dans un objet ou un motif, est l’invariance de l’objet ou du motif par une certaine transformation géométrique.
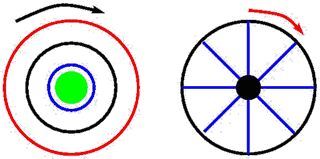
Motif à symétrie radiale (à gauche) et motif symétrique à 8 branches (à droite).
Par exemple, un motif à symétrie radiale est invariant par toute rotation. En revanche, un motif à 8 branches ne sera plus invariant par toute rotation, mais seulement par celles envoyant une branche sur une autre, c’est-à-dire les rotations d’angle multiple de π/4 (en radians, c’est-à-dire 45°). La symétrie de ce motif est donc entièrement caractérisée par l’ensemble des rotations le laissant invariant.
La généralisation à n branches (invariance par rotation d’angle multiple de 2π/n) est facile à effectuer, de même que l’extension à des symétries plus compliquées (par exemple une alternance régulière de branches de couleurs ou de formes différentes).
Un objet parfaitement uniforme (par exemple un plan) est invariant par toute translation. Un motif à rayures régulièrement espacées ne sera invariant que par un sous-ensemble de translations dans la direction transverse aux rayures, tout en restant invariant par toute translation parallèle aux rayures. La restriction pour un motif à carreaux est encore plus forte (voir la figure ci-dessous). La symétrie d’un motif à rayures ou à carreaux se formule plus souvent de façon « positive », comme l’existence de translations préservant le motif. Les motifs périodiques sont ainsi associés à des invariances par translation, avec une petite difficulté aux bords : la translation fait sortir l’objet de la région qu’il occupait ; on regardera plutôt des invariances locales, en considérant la transformation d’un échantillon, comme sur la figure ci-dessous.
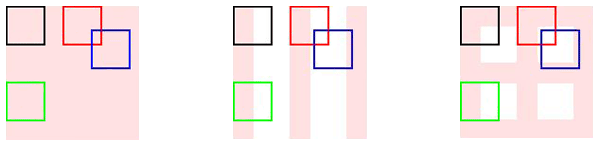
Comparaison des symétries présentées par différents motifs.
Un objet uniforme (à gauche) est invariant par toute translation. Un objet à rayures (au centre) est invariant par toute translation parallèle aux rayures : on observe le même motif dans le carré noir et dans le carré vert. Il est invariant seulement par certaines translations dans les autres directions : celles envoyant une rayure sur une autre, par exemple celle envoyant le carré noir sur le carré rouge. Les symétries d’un objet à carreaux (à droite) sont encore plus réduites : sur le schéma, seule la transformation envoyant le carré noir sur le carré rouge correspond à une symétrie du motif.
Plus il y a de transformations qui laissent invariant un motif, plus ce motif est symétrique. La symétrie la plus forte est observée dans une structure parfaitement homogène, autrement dit dans le cas d’une absence de motif, par exemple un plan uniformément gris. L’apparition d’une forme correspond à la brisure de cette symétrie maximale.
Quelles symétries pour le vivant ?
En particulier, la morphogenèse animale peut ainsi être vue comme une succession de brisures de symétrie à partir d’une cellule initiale sphérique, à mesure que celle-ci se multiplie et que les cellules filles s’organisent de façon structurée. C’est un problème très difficile, encore ouvert, que de comprendre ce qui détermine l’apparition de nouvelles structures et les changements de forme intervenant lors du développement de l’embryon. En particulier, une question cruciale est de discriminer ce qui est déterminé par les gènes, ce qui est au contraire déterminé par l’environnement, et ce qui résulte du hasard. Le problème est aussi difficile chez les plantes, pour comprendre par exemple ce qui détermine l’apparition de branches sur une tige linéaire, les symétries observées dans le positionnement des embranchements et des feuilles le long de la tige, ou le nombre de sépales et de pétales des fleurs.
Une démarche classique pour analyser la part de contrôle génétique de la morphogenèse et des symétries associées est d’étudier les exceptions et les défauts de développement de l’embryon quand on inactive certains gènes. Ce que faisaient les savants avant le développement des techniques d’ingénierie génétique était d’observer les anomalies spontanées ou celles qui apparaissent à la suite de l’application d’une perturbation extérieure. Certaines affectent la viabilité de l’individu. D’autres n’apparaissent comme des anomalies qu’au sens où elles sont observées chez un nombre moindre d’individus : variabilité du nombre d’appendices chez les animaux, du nombre de pétales chez les fleurs.

À la différence des cristaux, les organismes vivants peuvent présenter une symétrie d’ordre 5, par exemple les étoiles de mer et les oursins.
Photo : © William Scot / Wikimedia Commons.
Les symétries observées dans le vivant sont très différentes de celles des cristaux qui, elles, découlent de leur organisation régulière à l’échelle atomique. On montre qu’un réseau cristallin simple (corps pur) ne peut présenter que des symétries d’ordre 2, 3, 4 ou 6, mais jamais une symétrie d’ordre 5. En revanche, la symétrie d’ordre 5 est présente dans le vivant, par exemple chez les étoiles de mer et les oursins, voir la photo ci-contre. On a découvert récemment (en 1982) des corps composés dont la structure, appelée un quasi-cristal, est ordonnée sans être périodique comme l’est un réseau cristallin. Leur spectre de diffraction – la méthode traditionnellement utilisée pour observer les propriétés d’un cristal – est discret, comme pour un cristal, mais il peut présenter une symétrie d’ordre 5. Mais elle n’a rien à voir avec la symétrie des étoiles de mer à cinq branches, qui trouve son origine dans le processus de morphogenèse. De la même façon, il existe beaucoup de fleurs à cinq pétales (par exemple le bouton d’or ou la mauve), parfois même avec de la variabilité (par exemple le camélia simple, qui peut avoir de cinq à neuf pétales suivant les individus).
Un mécanisme général de formation de motifs a été proposé par le mathématicien Alan Turing en 1952 (voir le numéro de DocSciences qui lui est consacré). Turing introduit alors un modèle mathématique pour décrire la conjonction de réactions locales entre deux espèces chimiques et de leur diffusion moléculaire (le mouvement aléatoire des molécules résultant de l’agitation thermique). Dans certains régimes, le mélange homogène des deux espèces est instable, et la dynamique fait apparaitre des inhomogénéités de concentrations. De façon remarquable, celles-ci forment des motifs périodiques où la concentration d’une des espèces domine par rapport à l’autre. La période de ces motifs est fixée par la dynamique. Seule leur nature, en bandes ou en taches, dépend de la géométrie du système. Ce mécanisme est observé expérimentalement dans des systèmes chimiques. Il est aussi invoqué pour expliquer certains motifs périodiques observés dans le vivant : motifs sur le pelage ou la peau de certains animaux (guépard, zèbre, poisson-ange), positionnement des bourgeons de plumes chez le poulet, organisation en rosettes des feuilles le long de la tige de certaines plantes (aspérule).

On peut expliquer par un modèle mathématique les motifs du pelage de certains animaux, comme le guépard. Le motif en taches régulières se transforme en motif à bandes régulières dans la queue, plus longue que large. Photo : Thaïs Kjellberg.
Le modèle de Turing est souvent appelé équation(s) de réaction-diffusion, car il correspond au « croisement » d’une équation de diffusion (loi de Fick) et d’équations de la cinétique chimique (loi de l’action de masse). Une équation de réaction-diffusion est en général de la forme ∂a/∂t = D Δa + F(a) pour une concentration a(x,t), où F(a) est le terme de réaction (purement local) et D Δa le terme de diffusion, responsable du couplage spatial (Δ est l’opérateur Laplacien et D le coefficient de diffusion). Le modèle de Turing est un peu plus compliqué, car il fait intervenir deux espèces chimiques donc deux concentrations a(x,t) et b(x,t). Ce modèle a été abondamment repris depuis dans les contextes les plus variés, pour rendre compte de la formation dynamique de certains motifs et structures spatiales régulières.
De façon plus générale, la morphogenèse des organismes vivants est un processus se déroulant au cours du temps. On comprend alors comment les formes qui en émergent peuvent être en grande partie contrôlées par les gènes, par le fait que ceux-ci contrôlent les paramètres cinétiques du développement. L’identification des processus ou des contraintes à l’origine des motifs et de leurs symétries est souvent éclairée par l’étude des exceptions ou de la réponse à des perturbations. On étudiera par exemple la reconstitution du motif du pelage après une blessure de la peau, ou les différences observées chez des animaux jumeaux.
La morphogenèse des plantes – la phyllotaxie – est également un immense champ de questions et d’investigations. Une piste actuellement très explorée est l’étude de ce qui se passe au niveau de l’extrémité en croissance (ce qu’on appelle le méristème), au niveau directement observable à la loupe mais aussi en étudiant les échanges d’hormones végétales au niveau moléculaire ou les contraintes mécaniques au niveau cellulaire. On peut relier le positionnement des feuilles (appariées ou alternées, superposées ou au contraire décalées le long de la tige) à l’efficacité de la photosynthèse. L’efficacité en termes de pollinisation et de dispersion des graines est aussi intervenue, lors de l’évolution, dans la sélection (naturelle) des formes végétales et des processus sous-jacents, dans la mesure où ils sont en partie contrôlés par les gènes. Là aussi, les symétries s’expliquent par un compromis entre les contraintes mécaniques ou géométriques et le processus biologique de la croissance. Par exemple, on peut compter le nombre de spirales droites et le nombre de spirales gauches que tracent les inflorescences d’un tournesol ou les écailles d’une pomme de pin.


Le nombre de spirales droites et le nombre de spirales gauches que tracent les inflorescences d’un tournesol ou les écailles d’une pomme de pin forment une paire particulière, ce qui provient des contraintes géométriques s’exerçant lors de la croissance.
Photos : © Unclesam – Fotolia.com / © Vladimir Karpenko – Fotolia.com.
On peut vérifier en se promenant dans un champ ou une forêt que ces nombres sont toujours de la forme (ni, ni+1) où ni est le terme de la suite de Fibonacci définie par la récurrence: ni+1 = ni + ni-1. Les seules exceptions sont des individus malformés à la suite d’une perturbation (obstacle, agression par un insecte). L’explication (voir en particulier les travaux de Y. Couder et S. Douady) repose sur l’apparition séquentielle des bourgeons : une nouvelle inflorescence ou une nouvelle écaille se développe dès qu’il y a suffisamment de place disponible dans le méristème. Cela suffit à contraindre leur positionnement et à rendre compte des régularités observées.
Comprendre l’origine des symétries
L’étude mathématique de la morphogenèse et des symétries associées repose sur des équations aux dérivées partielles, les équations de réaction-diffusion mentionnées ci-dessus, qui ne peuvent être résolues que par des méthodes numériques sur ordinateur. On parle alors de simulation. Mais ce même terme est utilisé dans d’autres démarches de modélisation qui mettent en œuvre des types de modèles assez différents, le plus souvent de nature discrète, par opposition aux variables continues, temps ou espace, des équations aux dérivées partielles. Plutôt que de rendre compte des mécanismes par des systèmes d’équations mathématiques, il s’agit ainsi de décrire un par un, dans un programme informatique, les ingrédients et les processus élémentaires en jeu dans la morphogenèse, puis d’exécuter ce programme pour observer et mieux comprendre les structures qui en émergent, en particulier l’origine des symétries. Automates cellulaires, L-systèmes et systèmes multi-agents sont trois exemples particulièrement importants de ce type de modélisation.

Formation de motifs en spirale dans un automate cellulaire à deux dimensions, où une case a trois états possibles. Les règles du modèle prescrivent comment l’état d’une case change à chaque pas de temps en fonction de l’état des cases voisines.
Simulation de Christoph Fretter et Marc-Thorsten Hütt, Jacobs University, Brême.
Une première classe de simulations est celle des automates cellulaires. L’idée a été introduite par Von Neumann et abondamment développée depuis (citons le « jeu de la vie » de J. Conway et la classification des différents automates à une dimension en fonction de leur comportement, réalisée par S. Wolfram). Conçus dès le départ pour être implémentés sur un ordinateur, ces modèles sont entièrement discrets (en temps, en espace, en états) : on fixe un pas de temps régulier, la simulation se fait sur une grille découpant l’espace en cases ou cellules identiques, et chaque case ne peut prendre qu’un nombre fini d’états. On se donne ensuite des règles simples de dynamique, typiquement la façon dont une cellule change d’état en fonction de l’état de ses voisines.
Par exemple, dans le cas d’un automate à deux états (noir ou blanc), une case blanche devient noire au pas suivant si plus de la moitié de ses voisines sont noires, et une cellule noire devient blanche si plus de la moitié de ses voisines sont blanches. Ces règles sont appliquées récursivement à chaque pas de temps. Bien qu’elles soient très simples, elles produisent une variété étonnante de motifs, réguliers pour certaines règles et totalement imprédictibles pour d’autres (voir la figure ci-contre).
Une autre classe est formée par les L-systèmes, des algorithmes de croissance introduits par A. Lindenmayer pour reproduire la croissance des plantes. Ici aussi, on se donne des règles décrivant comment une tige croît, puis se divise pour donner deux ou plusieurs branches, qu’on applique récursivement. D’autres algorithmes assez similaires sont utilisés pour engendrer des structures fractales, c’est-à-dire des structures qui présentent des motifs répétés et identiques à toutes les échelles (on parle d’auto-similarité).
Une dernière classe plus récente car plus coûteuse en temps de calcul, est celle des modèles multi-agents ou individu-centrés. Ici, le modèle est constitué d’éléments – les agents – décrits par quelques caractéristiques simples, par exemple leur position dans l’espace, leur taille, leur vitesse, leur état interne (en général un nombre fini d’états possibles, par exemple actif ou inactif). On prescrit ensuite des règles locales d’évolution et d’interactions de ces agents, par exemple comment ils se nourrissent, croissent, se divisent, changent d’état au contact d’autres agents, intègrent l’état de l’environnement autour d’eux, etc. Les modèles de ce type sont d’une grande flexibilité, limitée seulement par la puissance de l’ordinateur. Ils permettent de prendre en compte de nombreux ingrédients (un risque à éviter est de se retrouver avec un modèle aussi complexe que la réalité, qui n’aide guère à dégager les mécanismes dominants). Ils sont souvent préférés aux automates cellulaires car ils évitent certains artefacts venant d’une trop grande simplification (en particulier les symétries artificielles produites par la discrétisation de l’espace en grille régulière et la synchronisation des changements locaux, effectués simultanément à chaque pas de temps).
Un des avantages de ces expérimentations numériques est de pouvoir faire varier indépendamment chaque paramètre du modèle, ce qui permet d’apprécier l’impact de chacun d’eux sur le processus de morphogenèse et sur les propriétés des motifs en résultant. Un autre avantage est d’être (maintenant) facilement réalisables sur un petit ordinateur personnel !
Newsletter
Le responsable de ce traitement est Inria. En saisissant votre adresse mail, vous consentez à recevoir chaque mois une sélection d'articles et à ce que vos données soient collectées et stockées comme décrit dans notre politique de confidentialité
Niveau de lecture
Aidez-nous à évaluer le niveau de lecture de ce document.
Votre choix a été pris en compte. Merci d'avoir estimé le niveau de ce document !

Annick Lesne