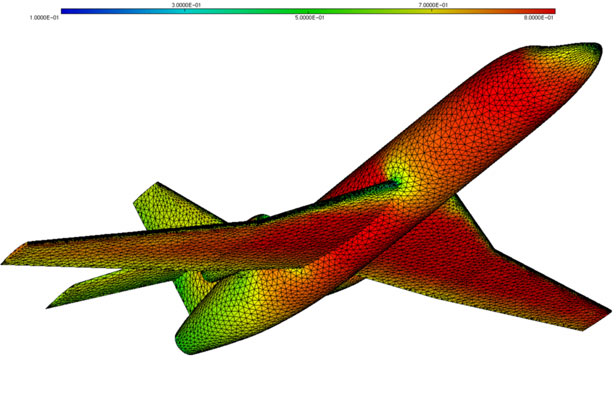
Les facettes du maillage

Visualisation du champ de vitesse autour d’un avion (Falcon – Dassault Aviation).

La résolution de problèmes physiques ou mécaniques sur un ordinateur nécessite une représentation de l’objet étudié et de son environnement. Pour décrire la forme d’un avion, par exemple, on ne peut pas simplement donner la position de chaque point de sa surface et y décrire la courbure du fuselage, car il y en a une infinité ! On est donc amené à proposer une approximation de la surface réelle de l’objet étudié, par la juxtaposition d’une multitude de petites facettes planes, faciles à décrire. C’est ce qu’on appelle un « maillage ». Plus on utilise de facettes, de « mailles », plus la représentation peut être fidèle. Mais il s’agit aussi d’en limiter le nombre, pour ne pas aboutir à une représentation trop complexe qui impliquerait des temps de calcul importants lors de la simulation. C’est le problème de l’optimisation des maillages, qui dépend aussi de l’utilisation qu’on souhaite en faire.

Du continu au discret

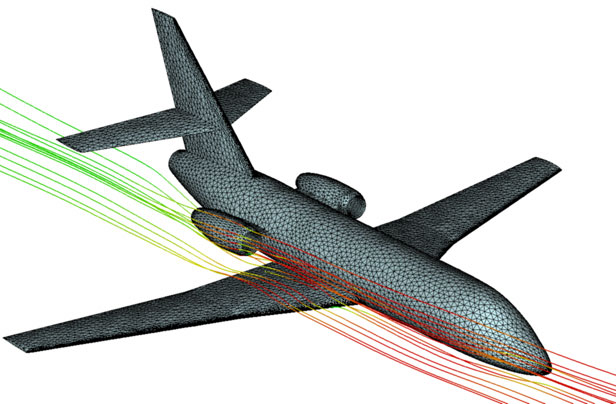
Supposons que l’on veuille étudier l’empreinte sonore d’un tel avion en déplacement supersonique : les lieux où l’on entendra le fameux « Bang ! ». Pour cela, il faut résoudre les équations mathématiques qui rendent compte de l’évolution de la vitesse et de la pression de l’air en tout point de l’espace qui entoure l’appareil. Mais cette perception continue de l’espace n’est pas directement exploitable dans un programme informatique qui effectue les calculs pas à pas. Il est donc nécessaire, là encore, de passer d’une description continue, donnée par les équations, à une description discrète où l’espace qui entoure l’avion est découpé en cellules élémentaires, l’équivalent des mailles précédentes, mais ici tridimensionnelles.

Des maillages adaptés

Des algorithmes spécifiques permettent de générer ces découpages de manière systématique. L’important est d’obtenir un maillage qui s’appuie effectivement sur la forme de l’avion, mais qui soit également adapté au problème étudié. Dans notre exemple, il faudra obtenir des mailles très serrées au voisinage des ondes de choc (responsables du bang, justement), car la densité de l’air y varie de manière très abrupte, et il faut donc y suivre ces variations millimètre par millimètre. En d’autres endroits, au contraire, des mailles beaucoup plus grandes seront suffisantes. Tout l’art consiste à identifier des algorithmes capables de produire ce type de maillages adaptés dans des situations très diverses, rapidement et automatiquement, avec un contrôle de la qualité du maillage obtenu.

Dans un cas réaliste, il faudra en outre coupler le maillage de l’air autour de l’avion avec celui de l’avion lui-même, ce qui permettra d’étudier les déformations sous la pression de l’air, ainsi qu’avec un maillage de l’atmosphère située entre l’avion et le sol, afin de calculer l’empreinte sonore au niveau des habitations. Les ingénieurs seront alors en mesure d’étudier, au moyen d’un algorithme d’optimisation, quelle forme il faut donner à l’avion pour réduire les nuisances sonores, par exemple en étirant le nez, en aplatissant l’habitacle ou en modifiant le point d’implantation des ailes ou leur angle d’ouverture.