
Les jeux à la rescousse de la vérification
La vérification est un domaine de l’informatique ayant pour objectif d’assurer la sûreté d’un système logiciel (un programme informatique par exemple) ou matériel (un processeur d’ordinateur), c’est-à-dire que celui-ci fait bien ce que l’on veut. C’est particulièrement crucial pour des systèmes critiques, c’est-à-dire dont les défaillances causeraient des conséquences dramatiques, tant financières, humaines qu’environnementales. La vérification, c’est donc les techniques mises en œuvre pour éviter les bugs, ces fameux écrans bleus ou arrêts inopinés d’un logiciel (ce qui n’arrive, bien sûr, que le jour où nous avions oublié d’enregistrer récemment notre travail !).
Certains bugs sont devenus célèbres. Celui du lecteur MP3 Zune par exemple, pour lequel tous les appareils se sont arrêtés le 31 décembre 2008 après minuit, mais ont repris leur marche normale dans la nuit du 1er au 2 janvier 2009 : le programme calculant l’année s’est retrouvé bloqué dans une boucle infinie du fait que 2008 était la première année bissextile depuis le lancement du lecteur Zune (cf figure 1 ci-dessous). Un autre bug célèbre, autrement plus coûteux, est celui d’Ariane 5, lors de son lancement inaugural le 4 juin 1996. Après 37 secondes de vol, la fusée a braqué entraînant sa dislocation partielle, suivie d’un déclenchement de son système d’autodestruction, détruisant au passage les coûteux satellites qu’elle transportait. C’était cette fois-ci une erreur de codage des nombres flottants — ces nombres permettent d’approcher les nombres réels afin de pouvoir les représenter sur ordinateur : leur utilisation entraîne le plus souvent de petites erreurs d’approximation, à l’exception des nombres très grands ou très petits en valeur absolue pour lesquels l’erreur est grande, ainsi que des erreurs d’arrondis lors des calculs — à l’origine de ce dysfonctionnement. Un dernier bug tristement célèbre est celui qui a touché la machine de radiothérapie Therac- 25 et a provoqué la mort de plusieurs patients par irradiation massive dans les années 1980 : c’était cette fois le logiciel servant d’interface entre l’opérateur humain et la machine qui contenait un bug.
|
|
# jours : nombre entier de jours depuis le 1er janvier 1980 année = 1980 while jours > 365: if bissextile(année): # fonction bissextile supposée écrite if jours > 366: jours -= 366 année += 1 else: jours -= 365 année += 1 |
Figure 1 : À gauche, le lecteur Zune de Microsoft et à droite, le morceau de programme critique qui calcule le numéro du jour (entre \(1\) et \(365\) ou \(366\)) en fonction du nombre de jours depuis le 1er janvier 1980. Vous pouvez tester ce programme avec jours valant initialement \(10 592\) puis \(10 593\) pour voir arriver l’erreur, et enfin \(10 594\) pour comprendre la résolution du bug consistant à attendre la fin de la journée. Crédit Photo stevekass via Flickr. |
|
Des méthodes formelles ont été développées pour limiter ce genre de bugs critiques. Elles passent par une spécification des propriétés que doivent satisfaire les systèmes en question. Le test de programmes permet de découvrir des bugs, pour cela il suffit que le programme échoue au test, mais ne permet pas de garantir l’absence de bugs : le test peut ne pas porter sur un bug présent dans le programme considéré. Des méthodes mathématiques permettant de prouver la correction des systèmes sont donc indispensables : on souhaite ainsi s’assurer que toute exécution du système satisfait la spécification formellement décrite. La recherche automatique de telles preuves de sûreté est l’idée de base du model checking, un domaine de recherche récompensé par un prix Turing en 2007 attribué à Edmund Clarke, Allen Emerson et Joseph Sifakis (ce dernier a réalisé ses recherches en France). L’idée fondamentale est d’abstraire le système à vérifier, par exemple le programme écrit dans un certain langage de programmation, pour considérer une représentation sous forme de graphe : les sommets du graphe sont les états du système à un instant donné (par exemple, la ligne du programme Python qu’on s’apprête à exécuter ainsi que la valeur de toutes ses variables) et les arcs du graphe représentent les évolutions possibles du système (lorsqu’on exécute l’affectation année = 1980 ou année += 1, on passe à la ligne suivante du programme et la valeur de la variable année a été modifiée). Un exemple de telle modélisation est donné ci-dessous (voir la figure 2). Le model checking consiste alors à vérifier que tout chemin dans ce graphe (c’est-à-dire toute exécution du programme) satisfait une propriété : par exemple, si l’on visite à un certain moment un sommet où une requête est envoyée à un serveur informatique, alors dans le futur, le serveur répond à la requête. Ces spécifications sont souvent décrites formellement dans des logiques temporelles, permettant de raisonner formellement sur l’enchaînement des actions du système. L’exemple précédent pourrait alors s’écrire \(G\)(requête \(⇒\) \(F\) réponse) signifiant qu’à tout moment (\(G\)lobalement), l’apparition d’une requête implique (\(⇒\)) que dans le \(F\)utur une réponse sera apportée. D’autres opérateurs (comme \(G\) et \(F\) dans l’exemple précédent) permettent de spécifier des propriétés sur l’enchaînement des événements dans le système.
1 while x == 1: 2 if y == 1: 3 x = 0 4 y = 1 - x 5 pass |
 |
Figure 2 : Un programme Python où les variables x et y prennent les valeurs \(0\) ou \(1\) initialement, et une représentation sous forme de graphe de l’évolution du programme : chaque sommet, autre que le sommet initial à gauche représentant l’instant avant qu’on ne démarre l’exécution, est étiqueté par un triplet (\(ℓ\), \(n\)x, \(n\)y) où \(ℓ\) est le numéro de la ligne du programme qui va être exécutée et \(n\)x, \(n\)y sont les valeurs respectives des variables x et y. À partir de cette vision graphique du programme, on peut s’apercevoir que la ligne \(4\) est inutile (et une ligne inutile est souvent le témoin que le programmeur n’a pas tout à fait compris ce qu’il avait écrit) : en effet, lorsqu’on atteint la ligne \(4\), la valeur de y est toujours différente de celle de x ce qui implique que l’affectation ne change rien à la valeur de y. On peut aussi s’apercevoir qu’il existe des exécutions de la boucle while qui ne terminent pas, où le programme boucle indéfiniment : c’est le cas lorsqu’on commence avec la valeur \(1\) pour x et \(0\) pour y. |
|
A priori, les graphes modélisant des programmes peuvent posséder un ensemble infini de sommets, typiquement lorsque les variables peuvent prendre des valeurs arbitrairement grandes. Cela rend très difficile l’étude de ces graphes en général. À titre d’exemple, le fameux problème de Syracuse s’intéresse à la terminaison de la boucle décrite (voir la figure 3 ci-dessous) quelle que soit la valeur initiale de la variable x. Même pour ce programme très simple, on ne connaît pas la réponse, et donc encore moins de technique permettant de répondre automatiquement à cette question : on sait même en fait qu’il n’existe pas de programme permettant de résoudre ce problème (c’est l’indécidabilité du problème de l’arrêt étudiée initialement par Alan Turing). Dans la suite, pour pallier cette impossibilité, on se limite à des graphes finis de systèmes. Cela demande souvent d’abstraire les valeurs entières ou flottantes, pour se limiter à un domaine fini de valeurs.
1 while x != 1: 2 if x % 2 == 0: 3 x = x // 2 4 else: 5 x = 3 * x + 1
|
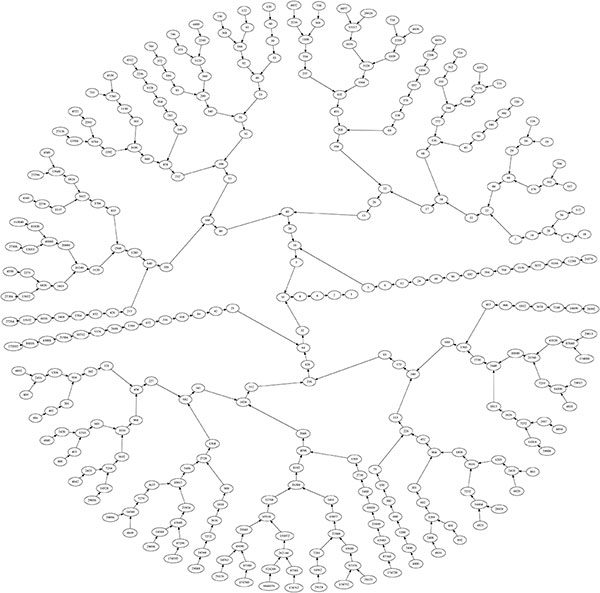 |
Figure 3 : Le problème de Syracuse s’intéresse à la terminaison du programme à gauche, quelle que soit la valeur initiale de la variable x. On a représenté à droite une petite partie du graphe infini de ce système si l’on ne connaît pas la valeur initiale de x : au centre, se trouve la valeur initiale \(1\) qui permet de sortir de la boucle. Pour zoomer dans l’image afin de voir le trajet suivi quand on part d’un entier ou d’un autre, cliquez ici. |
|
De la vérification à la synthèse
La technique du model checking est mature : de nombreux outils académiques et industriels ont été mis au point et permettent de vérifier des systèmes critiques variés. Les scientifiques tentent désormais d’aller plus loin, en limitant la source principale de bug dans les systèmes : l’intervention humaine. En effet, un bug n’est pas tant un problème du logiciel ou du matériel que la conséquence d’une erreur humaine de conception. Si l’on amoindrit le rôle de l’humain, on diminue les chances de produire des bugs. L’utopie rêvée par les héritiers du model checking est la synthèse automatique. Dans ce cas, on part d’un système partiellement décrit, où certaines parties non critiques du logiciel ont été écrites manuellement, mais où il reste des sections à écrire : on modélise ce système partiel à l’aide d’un graphe dans lequel certaines actions ne sont pas encore fixées (il y a donc un choix à faire entre plusieurs arcs). L’objectif est alors de produire automatiquement un modèle entièrement décrit qui satisfait une spécification : l’écriture de la spécification est laissée à l’humain, dans l’idée (discutable) qu’une spécification est plus aisée à écrire que le programme lui-même. On parle souvent de synthèse de contrôleur : le rôle du contrôleur, qui n’est donc pas un humain, est de guider l’évolution du système afin de satisfaire la spécification. Il ne peut pas contrôler la totalité du système qui est le plus souvent ouvert sur le monde extérieur : par exemple, une fusée doit pouvoir interagir avec des éléments extérieurs (la tour de contrôle) et son environnement (au travers de capteurs : vitesse, altitude…). On cherche donc à décrire un contrôleur qui permettra de satisfaire la spécification quelle que soit la façon dont évoluent les éléments extérieurs. D’autres travaux traitent de synthèse de programme, en utilisant des techniques radicalement différentes.
L’analogie avec un jeu devient alors flagrante : le contrôleur et son environnement peuvent être vus comme deux joueurs, se défiant sur une arène dont les règles du jeu sont dictées par le graphe du système partiellement décrit et la condition de gain pour le contrôleur est donnée par la spécification à satisfaire. Les sommets du graphe sont souvent distribués au joueur, permettant à chacun de jouer à son tour, de la même façon qu’aux échecs on alterne entre un tour du joueur Blanc et du joueur Noir. À son tour, le joueur qui possède le sommet où le système se trouve décide quel arc il utilise pour passer au sommet suivant.
Notons que, dans ce paradigme, l’environnement est un joueur parfaitement antagoniste, dont l’unique objectif est de faire échouer le contrôleur : cela permet de s’assurer que même dans le pire des cas possibles, le système critique ne rencontrera jamais de problème. La synthèse de contrôleur revient alors à trouver, automatiquement si possible, une stratégie gagnante du contrôleur dans ce jeu, c’est-à-dire une recette que le joueur contrôleur doit suivre, lui garantissant de gagner toute partie qu’il jouera contre l’environnement. Si l’on pense à la synthèse du programme d’un bras robotique utilisé le long d’une chaîne de production, le contrôleur a la responsabilité de déplacer le bras selon les contraintes physiques et peut-être aussi la vitesse du tapis roulant face à lui, alors que l’environnement gère l’arrivée d’objets sur la chaîne de production et les éventuelles interruptions du tapis roulant dues aux parties de la ligne qui suivent le bras robotique. La spécification du bras robotique, c’est-à-dire la condition de gain pour le contrôleur, pourrait être de trier les objets par couleur, en les déplaçant sur des tapis identifiés par les couleurs possibles (cf Figure 4).
 |
Contrôleur : bras robotique et vitesse du tapis roulant Environnement : choix de la couleur et de la position des pièces qui arrivent, arrêt du tapis roulant Objectif : trier les pièces par couleur |
Figure 4 : Description d’une tâche de synthèse du contrôleur d’un bras robotique sur une chaîne de montage. Source : Public Domain Vectors. |
|
Le défi est donc de trouver des algorithmes permettant de synthétiser automatiquement de telles stratégies gagnantes pour le contrôleur. C’est un domaine scientifique que l’on appelle la théorie algorithmique des jeux. Non seulement, comme on peut le faire en théorie des jeux appliquée à la biologie ou l’économie, on étudie l’interaction d’agents rationnels qui s’affrontent le long de ce qu’on appelle un jeu, mais en plus on insiste sur la capacité, ou non, de pouvoir réaliser cette étude automatiquement, sans intervention humaine.
Le jeu des pirates
Illustrons cela à l’aide d’un exemple. Imaginons un groupe de cinq pirates qui vient de découvrir un trésor contenant \(100\) pièces d’or. Les pirates sont organisés suivant un ordre hiérarchique simple : la capitaine Élisa, un quartier-maître Dorian, une timonière Cora, son second Barny et tout en bas de l’échelle le matelot pingouin Atchoum. La répartition du butin se réalise en plusieurs phases, résumées dans la figure 5 ci-dessous. Dans un premier temps, la capitaine propose une répartition entre les cinq pirates, puis tout le monde vote (oui ou non) et si au moins la moitié des pirates est d’accord avec la répartition, celle-ci est effectuée et la distribution s’arrête. Sinon, la capitaine est jetée aux requins et c’est son quartier-maître qui devient capitaine et propose à son tour une répartition. À nouveau, tout le monde vote et la répartition n’est actée que si au moins la moitié des pirates est d’accord. Et ainsi de suite, jusqu’à ce qu’une distribution soit acceptée.
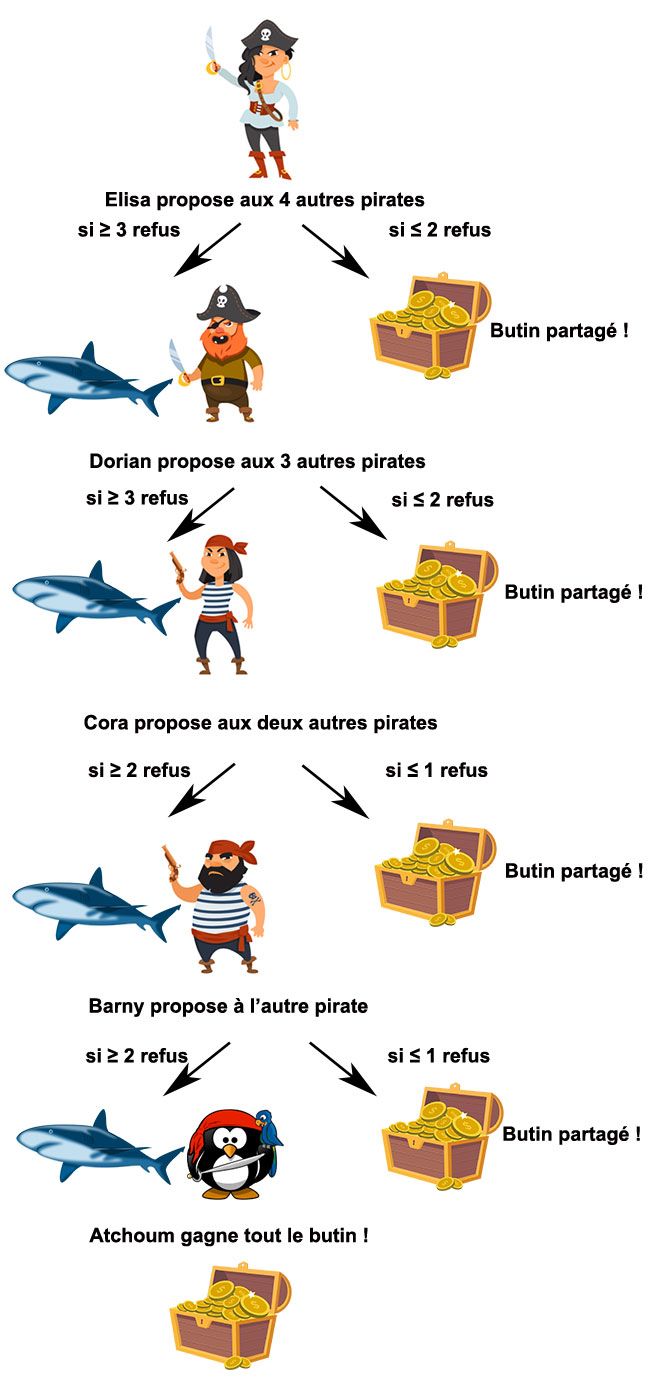
Figure 5 : Jeu des pirates. Illustrations Adobe Stock / Public Domain vectors.
Prenons le point de vue de la capitaine Élisa. Son objectif est non seulement de survivre, mais aussi de conserver la plus grande part possible du butin : en termes de vérification de système, la spécification (survivre) est donc complétée par une mesure à optimiser (ici le butin, mais on pourrait imaginer vouloir minimiser l’énergie dépensée ou maximiser la probabilité de succès, dans d’autres situations). Quelle proposition doit-elle ainsi proposer ? Avant de continuer votre lecture, prenez le temps d’y réfléchir un peu…
Dans la mesure où il n’y a qu’un nombre fini de possibilités de répartition, on pourrait naïvement les générer toutes et simuler les règles du jeu pour en déduire la proposition optimale. Cependant le nombre de possibilités est très grand en pratique (c’est le nombre de Stirling de seconde espèce, qui grandit exponentiellement en fonction du nombre de pirates et du nombre de pièces) et l’approche naïve n’aboutit donc pas. Il nous faut trouver mieux, en réfléchissant un peu…
Puisqu’il faut qu’elle convainque au moins deux autres pirates (pour obtenir une majorité de trois voix, en comptant la sienne), on peut se dire intuitivement qu’elle va diviser le butin en trois environ et donner un tiers du butin à ses deux seconds, Dorian et Cora. Mais la question se pose alors de savoir si une telle répartition lui permet de rester en vie. L’un des deux protagonistes a-t-il intérêt à ne pas accepter cette proposition a priori généreuse ? Autre question, non moins importante pour la vénale Élisa : peut-elle imaginer une proposition plus intéressante pour elle que de ne conserver qu’un tiers du butin ?
Pour nous aider à y voir plus clair, appliquons un raisonnement (ressemblant à une récurrence) consistant à considérer une situation simplifiée à l’extrême puis à augmenter la difficulté petit à petit. Considérons d’abord le cas fort morbide où les trois premiers pirates ont été jetés aux requins, Barny et Atchoum étant les deux seuls pirates encore en vie. Puisque Barny ne va pas refuser sa propre proposition, il peut conserver la totalité du butin et ainsi spolier entièrement Atchoum : il conserve ainsi les \(100\) pièces d’or. Réintroduisons alors Cora dans l’histoire pour voir ce qu’elle a intérêt à faire en sachant la stratégie de Barny si elle venait à disparaître. C’est plus compliqué dans ce cas puisque Cora doit convaincre au moins l’un des deux autres pirates pour survivre. Le plus simple, pour elle, est de corrompre la seule pirate qui n’obtient rien dans le cas où Cora est jetée aux requins, c’est-à-dire Atchoum. Et nos pirates étant des êtres parfaitement rationnels, Atchoum se contentera d’une seule pièce d’or pour voter pour la proposition faite par Cora : celle-ci peut donc proposer la répartition consistant à conserver \(99\) pièces d’or et en donner \(1\) à Atchoum. Le pauvre Barny repart bredouille dans cette situation. Un raisonnement similaire permet de se convaincre qu’avec l’ajout du quatrième pirate Dorian, il lui suffit de corrompre le pirate percevant le moins de butin dans la situation précédente, à savoir Barny. Dorian peut donc proposer en toute sécurité de conserver \(99\) pièces d’or et en donner \(1\) à Barny. Finalement, cela permet d’en conclure la stratégie optimale pour Élisa : elle doit convaincre au moins deux autres pirates de voter pour elle, et elle a tout intérêt à corrompre les pirates qui ne touchent rien dans la situation précédente (où Élisa serait jetée aux requins). Il lui suffit donc de conserver \(98\) pièces d’or et de donner \(1\) pièce à Cora et \(1\) pièce à Atchoum. Élisa gagne alors bien plus que le tiers du butin, même si le partage est pour le moins inéquitable… Voici un tableau résumant les différentes étapes du raisonnement :
| Part d’Elisa | Part de Dorian | Part de Cora | Part de Barny | Part d’Atchoum | |
| Proposition d’Atchoum | 100 | ||||
| Proposition de Barny | 100 | 0 | |||
| Proposition de Cora | 99 | 0 | 1 | ||
| Proposition de Dorian | 99 | 0 | 1 | 0 | |
| Proposition d’Élisa | 98 | 0 | 1 | 0 | 1 |
À vous de poursuivre le raisonnement dans le cas où il y aurait un sixième, puis un septième pirate. Combien de pirates au maximum peut-il y avoir avant que la capitaine ne puisse plus s’assurer de survivre avec \(100\) pièces d’or ? On peut aussi considérer une variante du jeu où la capitaine doit obtenir une majorité stricte des voix pour survivre…
Résoudre les jeux pour la synthèse de contrôleur
La théorie algorithmique des jeux permet de généraliser ce genre de raisonnement par récurrence à des situations plus complexes. Dans l’application à la vérification, les jeux qui nous intéressent se déroulent sur des graphes (celui du système partiellement décrit) avec deux joueurs seulement (le contrôleur et l’environnement) qui jouent chacun leur tour, selon le joueur à qui appartient le sommet courant. Dans le cas relativement simple où l’objectif du contrôleur est d’éviter la survenue d’un bug (certains sommets cibles du graphe), on parle de jeu de sûreté. Pour résoudre ces jeux, on considère le point de vue de l’environnement qui a l’objectif antagoniste d’atteindre les sommets cibles de bug : on parle alors d’un objectif d’accessibilité. C’est là que le raisonnement par récurrence devient utile. Pour être sûr de gagner dans un certain sommet qui lui appartient, l’environnement doit pouvoir choisir un successeur dans lequel il peut gagner. Inversement, c’est le contrôleur qui gagne dans un sommet qui lui appartient si tout successeur de ce sommet est perdant pour l’environnement (et donc gagnant pour le contrôleur). En partant des sommets de bug (où l’environnement a gagné d’office), on peut donc propager sommet après sommet qui des deux joueurs peut gagner (ou ne peut pas empêcher de perdre). Ce genre de récurrence de théorie des jeux porte le nom d’attracteur, puisqu’on cherche tous les sommets où l’environnement peut attirer la partie dans un sommet cible de bug. Un exemple d’application de l’attracteur est présenté dans la figure 6 ci-dessous.
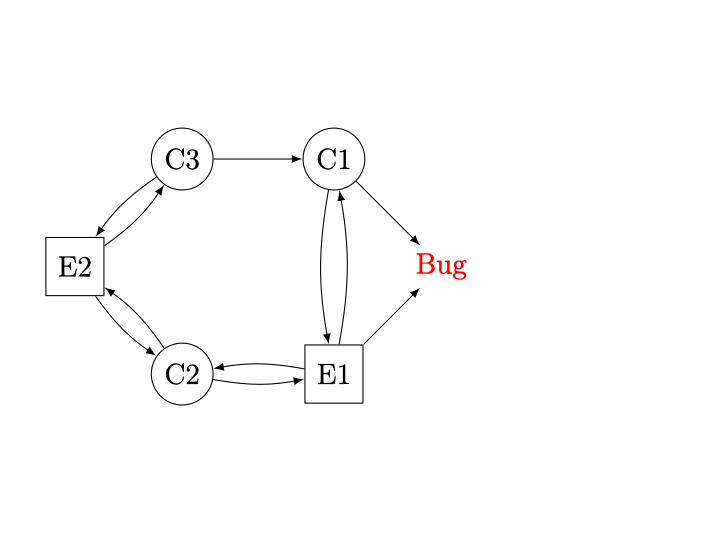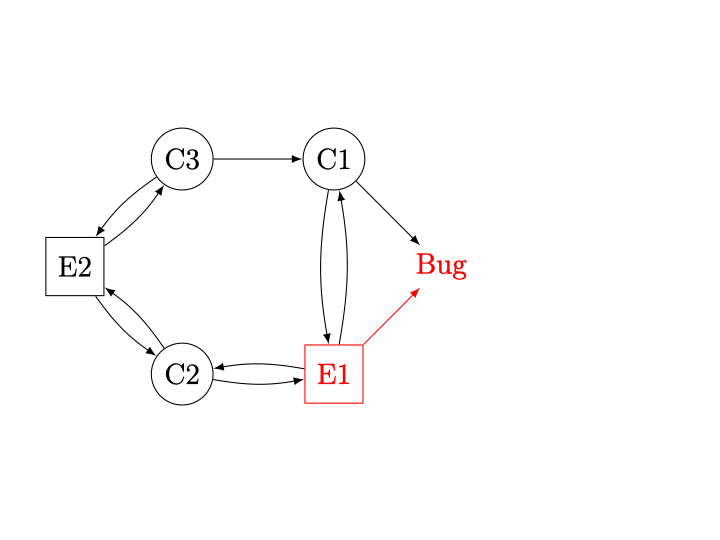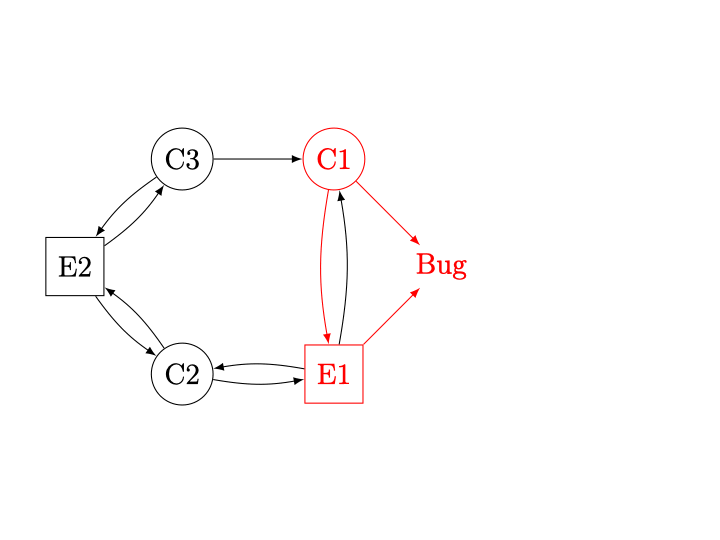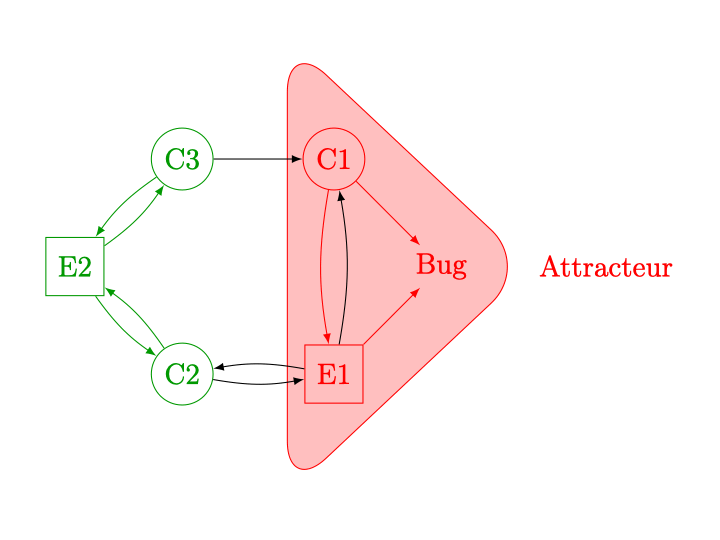
Figure 6 : Le contrôleur possède les trois sommets \(C\)1, \(C\)2 et \(C\)3, alors que l’environnement possède les sommets \(E\)1 et \(E\)2. Le sommet à droite est la cible, représentant le bug que souhaite éviter le contrôleur. À chaque étape du raisonnement par attracteur, on regarde si l’on peut conclure que l’environnement a une stratégie pour atteindre la cible ou si le contrôleur n’a pas d’autre choix que de l’atteindre aussi. Au début, on conclut de suite qu’en \(E\)1, l’environnement peut suivre l’arc menant au bug directement (même si l’on ne sait pas encore ce qu’il se passerait si l’environnement choisissait d’aller en \(C\)1 ou \(C\)2). Le sommet \(E\)1 est donc gagnant pour l’environnement. À partir de cette information, on peut étudier le sommet \(C\)1 du contrôleur : en effet, les deux choix possibles de successeur sont désormais déclarés gagnants pour l’environnement. Le contrôleur ne peut donc pas éviter de perdre en \(C\)1, quoi qu’il fasse. Le sommet \(C\)1 est donc aussi gagnant pour l’environnement. Le raisonnement par attracteur atteint cependant un point fixe puisqu’aucun des sommets restants ne peut être déclaré gagnant pour l’environnement : en \(C\)2 et \(C\)3, le contrôleur peut toujours aller vers un sommet (\(E\)2) non encore déclaré gagnant pour l’environnement, et en \(E\)2, quoi que fasse l’environnement il ne peut pas atteindre un sommet gagnant. On conclut alors que les sommets \(C\)2, \(C\)3 et \(E\)2 sont perdants pour l’environnement, c’est-à-dire gagnants pour le contrôleur : ce sont les états du système à partir desquels le contrôleur peut éviter le bug.
Ces techniques d’attracteur sont à la base de bien d’autres algorithmes permettant de résoudre des jeux avec des objectifs plus compliqués. Par exemple, certains systèmes critiques doivent pouvoir fonctionner sans interruption aussi longtemps qu’il plaira aux utilisateurs. Pensez à un ascenseur par exemple, qui ne doit jamais s’interrompre (sauf si c’est planifié par un humain responsable de son entretien). Il est alors plus simple de considérer que le système fonctionnera pendant un temps infini. Dans ce cadre, le contrôleur pourrait vouloir passer infiniment souvent par certains sommets cibles : cela veut dire que régulièrement, on doit visiter un sommet cible du graphe, ce qui peut servir à modéliser par exemple que, sous certaines bonnes hypothèses, un ascenseur passe régulièrement au rez-de-chaussée de l’immeuble, sans rester coincé à faire des navettes uniquement entre les étages supérieurs. Les attracteurs permettent de résoudre ces objectifs aussi puisqu’il s’agit pour le contrôleur d’atteindre un des sommets cibles, puis depuis ce sommet-là, trouver une stratégie pour y revenir une fois : il lui suffit alors de continuer à appliquer cette même stratégie pour y revenir aussi souvent qu’il le désire (et donc une infinité de fois si la partie durait un temps infini).
Des jeux à objectifs quantitatifs
D’autres cas où ces attracteurs sont fort utiles concernent des extensions quantitatives des jeux sur graphes. Le contrôleur souhaite satisfaire une spécification (par exemple atteindre un sommet cible) tout en minimisant les coûts pour y parvenir (ou en maximisant son butin, dans le cas des pirates). On parle de jeu de plus court chemin puisque le contrôleur cherche finalement à produire un plus court chemin vers un sommet cible, quel que soit le comportement de l’environnement. Dans le cas à \(1\) joueur, il existe des algorithmes très efficaces pour résoudre ce problème que les coûts soient des nombres positifs (l’algorithme de Dijkstra suffit alors, plus de détails dans l’article « Le plus court chemin ») ou des nombres quelconques (l’algorithme de Bellman-Ford, par exemple, convient). Lorsqu’on a deux joueurs, on peut adapter ces idées, en intégrant les raisonnements par attracteurs, pour résoudre les jeux correspondants. Un exemple de jeu de plus court chemin et de sa résolution est décrit sur la figure 7 ci-dessous.

Figure 7 : Un jeu de plus court chemin avec deux sommets appartenant au contrôleur (\(C\)1 et \(C\)2) et deux sommets appartenant à l’environnement (\(E\)1 et \(E\)2). Pour le résoudre, on applique un algorithme proche de celui de Dijkstra. On commence par supposer que les distances à la cible sont initialement infinies. Ensuite, on considère les sommets proches de la cible. Dans le sommet \(C\)1, le contrôleur sait qu’il peut donc au moins garantir d’atteindre la cible avec un coût total de \(25\) (mais il peut sans doute faire mieux…). Dans le sommet \(E\)2, l’environnement conserve une distance infinie à la cible puisqu’il peut toujours choisir d’aller vers le sommet \(C\)2 qui a pour l’instant une distance infinie à la cible. Mais justement, le contrôleur s’aperçoit que dans le sommet \(C\)2, il peut désormais rallier la cible avec un coût de \(3\). On poursuit la visite des sommets du graphe. Désormais l’environnement, dans le sommet \(E\)2, ne peut pas éviter la cible et doit choisir entre le coût \(0\) (arc allant directement à la cible) et le coût \(2\) \(+\) \(3\) (arc allant vers \(C\)2) : il préfère donc le second choix et la distance de \(E\)2 à la cible est donc de \(5\). On poursuit avec \(E\)1 qui préfère alors sélectionner l’arc vers \(E\)2, lui permettant d’obtenir une distance à la cible égale à \(6\). Finalement, dans \(C\)1, le contrôleur préfère donc changer sa décision et utiliser l’arc vers \(E\)1, lui garantissant une distance à la cible de \(8\) plutôt que \(25\).
Cependant, cela commence à devenir plus complexe en termes de temps de calcul, en particulier dans le cas de nombres quelconques (positifs ou négatifs) où l’on ne connait pas à ce jour d’algorithme résolvant le problème en temps polynomial (en fonction de la taille du jeu). Le meilleur algorithme connu à ce jour demande un temps pseudo-polynomial c’est-à-dire qui dépend (linéairement) des coûts dans le jeu, contrairement aux techniques d’attracteur vues précédemment et l’algorithme de Dijkstra qui ne dépendent (polynomialement) que du nombre de sommets dans le graphe. Cela reflète une particularité de ces jeux : le contrôleur nécessite de la mémoire pour jouer optimalement dans de tels jeux (cf figure 8 ci-dessous), c’est-à-dire que le contrôleur ne peut pas toujours suivre la même stratégie lorsqu’il passe par un certain sommet du graphe, il doit parfois suivre un arc et parfois un autre. C’est très différent des autres classes de jeux cités avant, où des stratégies sans mémoire (c’est-à-dire où le contrôleur n’a pas besoin de changer d’avis) suffisent.

Figure 8 : Dans ce jeu à trois sommets, le contrôleur, qui possède le sommet en haut à droite, souhaite atteindre la cible en bas tout en minimisant le poids total du chemin. Le raisonnement par attracteur se réalise ainsi. En un coup, le contrôleur sait qu’il peut atteindre la cible avec un coût total de \(0\). En deux coups, l’environnement apprend alors qu’il ne peut pas éviter la cible, mais préfère alors prendre l’arc pointillé pour ne donner que le coût total \(−1\) au contrôleur. Mais celui-ci peut alors changer d’avis et finalement choisir lui aussi d’utiliser l’arc pointillé une fois. En répétant ce raisonnement, le contrôleur et l’environnement s’aperçoivent tour à tour qu’ils peuvent garantir et ne peuvent empêcher, respectivement, un coût total de \(−2\), puis \(−3\), etc. jusqu’à \(−10\). (Notons que le nombre d’itérations nécessaires pour ce raisonnement est de l’ordre de \(10\), la plus grande valeur absolue des poids apparaissant dans le jeu.) L’environnement apprend alors finalement qu’il a tout intérêt à aller directement à la cible, dès le premier instant où le contrôleur lui donne sa chance. En résumé, depuis les deux sommets du haut, les deux joueurs parviennent à garantir un poids total de \(−10\) et pas mieux pour l’un ou l’autre. Cependant, le contrôleur a besoin de jouer avec mémoire pour garantir cela : en effet, s’il décide d’appliquer une stratégie qui prend toujours l’arc pointillé, alors l’environnement peut décider de ne finalement jamais aller à la cible, ce qui est la pire des situations possibles pour le contrôleur où la spécification ne sera même plus garantie.
Autres extensions
À partir de ces objectifs de base sur des jeux représentant des systèmes partiellement décrits, on peut considérer des extensions permettant de modéliser mieux les situations réelles à synthétiser. En particulier, beaucoup de systèmes critiques doivent agir en temps réel, et les spécifications peuvent donc intégrer ces aspects temporels : dans un système d’ABS gérant le freinage d’une voiture, il est ainsi important que l’appui sur la pédale de frein résulte dans le futur en le freinage de la voiture, mais on veut en plus que celui-ci intervienne relativement rapidement après, sans quoi l’accident est inévitable. D’autres extensions permettent de remplacer la mémoire, dont on a vu avant qu’elle pouvait être nécessaire pour jouer optimalement, par des tirages aléatoires. En effet, dans certains cas, on arrive à simuler la mémoire en utilisant un tirage aléatoire (avec une chance sur 10 suivre un arc, et avec 9 chances sur 10 d’en suivre un autre) : l’usage de probabilités est indispensable aussi dans d’autres domaines de la théorie des jeux, par exemple lorsqu’on souhaite trouver une stratégie optimale dans le jeu pierre-feuille-ciseaux (c’est-à-dire un équilibre de Nash dans un jeu donné sous forme stratégique, où toutes les combinaisons de stratégies des joueurs sont associées à une valeur gagnée par chaque joueur dans ce cas – voir l’article « Quand l’informatique rencontre les sciences économiques » sur les liens entre les équilibres de Nash et l’économie). Finalement, d’autres extensions considèrent les pannes que le système peut rencontrer au cours de son évolution : cela se modélise par la suppression dynamique de certains arcs dans le graphe, au moins pour un certain temps. Le contrôleur doit pouvoir dynamiquement mettre à jour sa stratégie dans ce genre de cas : des ponts ont ainsi commencé à être tracés avec la théorie évolutionnaire des jeux, un autre sous-domaine de la théorie des jeux s’intéressant à l’évolution des stratégies des protagonistes au cours du temps.
Newsletter
Le responsable de ce traitement est Inria. En saisissant votre adresse mail, vous consentez à recevoir chaque mois une sélection d'articles et à ce que vos données soient collectées et stockées comme décrit dans notre politique de confidentialité
Niveau de lecture
Aidez-nous à évaluer le niveau de lecture de ce document.
Votre choix a été pris en compte. Merci d'avoir estimé le niveau de ce document !

Benjamin Monmege
Maître de conférences au Laboratoire d'Informatique et Systèmes (LIS) à Aix-Marseille Université.

