L’ordinateur au cœur de la découverte mathématique

Image : RyGuy, Wikimedia Commons.
Dans les sciences expérimentales et appliquées, l’usage de l’ordinateur est omniprésent. Il est indispensable dans l’analyse des grandes quantités de données provenant des expériences ainsi que dans la simulation des systèmes complexes. Cette utilisation de l’outil informatique à des fins d’analyse et de calcul est bien connue, des projets tels que folding@home permettent même à chacun d’y participer modestement. On pourrait penser que les mathématiques, royaume des raisonnements abstraits, utilisent peu les calculs numériques. Or, depuis l’invention de l’ordinateur, les mathématiciens les ont utilisés à chaque étape du processus de découverte.
On peut schématiser ce processus comme suit. D’abord, le mathématicien énonce quelque chose qui lui semble être vrai : il formule une conjecture. Il tente ensuite d’établir avec certitude sa vérité ou sa fausseté. Si un contre-exemple est identifié, alors la conjecture est rejetée ou, éventuellement, reformulée. Par contre, si une preuve est trouvée, alors la conjecture devient un résultat mathématique, sous la forme d’un théorème. L’ordinateur est utilisé pour explorer, dériver ou infirmer des conjectures de manière interactive et parfois de manière totalement automatisée. Plus surprenant peut-être est l’importance croissante que l’ordinateur joue dans les preuves mathématiques. Pour étayer ce propos, développons deux exemples, l’un dans le domaine des mathématiques discrètes, l’autre dans celui des mathématiques continues.
Mathématiques discrètes

Carte coloriée avec 4 couleurs.
L’exemple le plus célèbre du rôle primordial joué par l’ordinateur dans une preuve mathématique complexe est sans conteste celui du théorème des quatre couleurs. Celui-ci affirme que « toute subdivision du plan en régions contigües peut être coloriée avec au plus quatre couleurs, de telle manière que deux régions adjacentes n’aient pas la même couleur ». Une telle subdivision du plan est une carte planaire.
Un exemple de carte est donné sur la figure ci-contre. Il est à noter que deux régions — comme par exemple certains états américains — ne se touchant que par un point ne sont pas dites adjacentes. On attribue la paternité de la « conjecture des quatre couleurs » au cartographe F. Guthrie qui fut capable en 1852 de colorier la carte des cantons d’Angleterre avec seulement quatre couleurs. Malgré la simplicité de l’énoncé, il faudra attendre plus d’un siècle pour qu’une preuve en soit donnée.
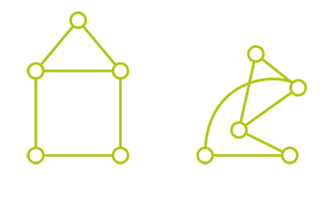
Deux représentations d’un même graphe.
Le théorème des quatre couleurs peut être énoncé de manière formelle grâce à la théorie des graphes. Un graphe est un objet mathématique constitué de sommets et de relations entre certaines paires de sommets (les arêtes). Un graphe se représente très facilement à l’aide de cercles (correspondant aux sommets) et de lignes joignant certaines paires de cercles (les arêtes). Dans un tel dessin, l’emplacement des cercles ou le fait qu’une ligne soit droite n’a pas d’importance. Seule la structure importe, c’est-à-dire la présence ou non d’une arête entre deux sommets donnés. Ainsi, deux représentations d’un seul et même graphe sont illustrées ici. Si un graphe peut être représenté de telle sorte que les lignes ne se croisent pas, on dit qu’il est planaire.

Correspondance entre une carte et un graphe planaire.
Toute carte planaire peut être modélisée par un graphe planaire : il suffit d’associer un sommet à chaque région et d’ajouter une arête entre deux sommets s’ils correspondent à des régions adjacentes. Voici par exemple une carte à quatre régions et le graphe associé.
Une coloration de graphe revient à colorier les sommets d’un graphe en s’assurant que deux sommets adjacents n’ont pas la même couleur. Le théorème des quatre couleurs devient : « tout graphe planaire peut être colorié avec au plus quatre couleurs ». Le graphe de la dernière figure possède une propriété intéressante par rapport à la coloration : il constitue le plus petit exemple montrant que trois couleurs ne suffisent pas. D’un point de vue cartographique, ce graphe modélise la situation du Luxembourg entouré par la Belgique, l’Allemagne et la France ; ces trois derniers pays étant deux à deux limitrophes.
Quatre couleurs sont donc nécessaires pour colorier n’importe quel graphe planaire. Il reste à prouver que quatre couleurs sont également suffisantes.
C’est seulement en 1976 que K. Appel et W. Haken proposent une preuve basée sur la notion de configuration réductible introduite par G. D. Birkhoff au début du XXe siècle.
Dans le cadre du problème de la coloration d’une carte (ou du graphe planaire associé), une configuration est un morceau de la carte qui satisfait une structure donnée. Par exemple, dans la figure ci-dessous, la partie de la carte incluant la France, la Belgique et le Luxembourg forme une configuration triangulaire dans le graphe associé.

On dit qu’une configuration est réductible si elle possède la propriété suivante : si la carte obtenue en supprimant la configuration peut être coloriée avec au plus quatre couleurs; alors la carte originale est également coloriable avec au plus quatre couleurs.
Ils identifient 1936 configurations particulières dont il faut montrer la réductibilité pour établir que tout graphe planaire est coloriable avec quatre couleurs. Ensuite, ils font appel à l’ordinateur (environ 50 jours de calculs à l’époque) pour vérifier que chacune de ces configurations est bien réductible. D’autres preuves ont suivi mais toutes ont requis l’aide de l’ordinateur : elles ne sont pas vérifiables « à la main » (ce qui a d’ailleurs provoqué la controverse). Ainsi, en 1997, N. Robertson, D. P. Sanders, P. D. Seymour et R. Thomas publient une nouvelle preuve n’utilisant plus que 633 configurations et automatisent également la première partie de la preuve permettant d’obtenir cet ensemble de configurations. En 2005, G. Gonthier et B. Werner écrivent une version formelle de la preuve de N. Robertson et de ses co-auteurs à l’aide du programme Coq développé en France par l’Inria.
Les graphes — qui modélisent bien d’autres situations concrètes que des cartes — constituent un exemple de structures discrètes qui, par définition et par essence, ne requièrent pas la notion de continuité. Les objets mathématiques discrets ont une particularité très utile : en général, il y en a une infinité, mais ils sont énumérables. Dans ce domaine, la machine surpasse de loin l’Homme et l’énumération est bien souvent à la base de l’aide apportée par l’ordinateur. C’est le cas par exemple du système GraPHedron, développé à l’Institut d’Informatique de l’UMONS (en collaboration avec l’ULB) et capable de générer des conjectures en théorie des graphes de manière interactive et, dans certains cas, entièrement automatique. Il est également utile dans la construction des preuves et a notamment permis de résoudre un problème mentionné comme ouvert depuis 1962.
Le nombre de stabilité d’un graphe G est le nombre maximum de sommets (choisis parmi tous les sommets de G) tel qu’il n’existe aucune arête entre ces sommets. En 1941, P. Turán publie un des théorèmes les plus célèbres de la théorie des graphes. Le théorème de Turán donne une réponse précise à la question suivante : parmi l’ensemble des graphes ayant un nombre de sommets n et un nombre de stabilité α donnés, quels sont les graphes qui minimisent le nombre d’arêtes ? À chaque paire de valeurs possibles pour n et α correspond un graphe particulier. Cette famille de graphes sont les graphes de Turán.
Un graphe est connexe s’il est possible de suivre un chemin (une succession d’arêtes) entre n’importe quelle paire de ses sommets. Les graphes de Turán ont la particularité de ne pas être connexes (sauf quand α = 1). La question suivante, posée par Ore en 1962, semble donc toute naturelle : quels sont les graphes connexes minimisant le nombre d’arêtes pour un nombre de sommets n et un nombre de stabilité α donnés ? La réponse n’a été publiée qu’en 2008 et a été obtenue à l’aide de GraPHedron. Cet outil a en effet permis de caractériser une famille de graphes constituant une variante connexe des graphes de Turán.
Mathématiques continues
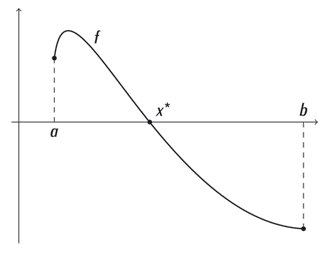
Racine d’une fonction.
L’ordinateur est également employé pour les mathématiques dites « continues ». Celles-ci apparaissent dans la modélisation d’un grand nombre de phénomènes physiques, économiques, ou industriels, notamment par le biais d’équations différentielles. Comprendre ces équations, pour le mathématicien, ne signifie pas simplement inférer les comportements de leurs solutions à partir de quelques calculs et simulations numériques. La certitude des connaissances mathématiques repose, en effet, sur des définitions précises et des chaînes de déductions sans faille.
Afin d’expliquer comment l’ordinateur peut y aider et quels sont les défis à relever, considérons un exemple de base : la preuve de l’existence de la racine d’une fonction. Notons f une fonction à valeurs réelles dépendant d’une variable x qui peut varier dans un intervalle [a, b]. On cherche une racine x* de f, c’est-à-dire un x* dans [a, b] qui annule f. Imaginons que f soit compliquée, rendant toute analyse « à la main » impraticable. Notons que très souvent, les fonctions dépendent de nombreuses variables, ce qui augmente encore la difficulté.
La première chose à remarquer est qu’il est impossible pour un ordinateur d’évaluer f en tous les points de l’intervalle [a, b] vu qu’il y en a une infinité. Heureusement, le théorème dit « des valeurs intermédiaires » affirme que, si f est continue et si f(a) et f(b) sont de signes opposés, alors f possède une racine dans [a, b]. Si la continuité de f doit être vérifiée par le mathématicien, on peut espérer utiliser un programme informatique pour évaluer f(a) et f(b). Or f n’est en général pas calculable exactement par un ordinateur. On le comprend facilement si on se rappelle que les ordinateurs ne peuvent travailler qu’avec un nombre fini de chiffres, alors que de simples opérations telles que prendre la racine carrée de 2 génèrent des nombres qui en possèdent une infinité. Ceci implique que les calculs sur ordinateur sont arrondis et, par conséquent, qu’on peut seulement estimer les valeurs de f(a) et f(b). La crainte est alors que l’accumulation de ces petites erreurs d’arrondi ne change le signe de f(a) ou f(b). Cette crainte est fondée : il existe des exemples de programmes retournant des résultats totalement erronés dû à l’amplification de ces erreurs d’arrondi.
Considérons la suite de nombres u0, u1, u2… définie par :
u0 = 3/2 = 1,5
u1 = 5/3 = 1,6666666…
un+1 = 2003 – 6002/un + 4000/un un-1
La suite tend vers 2 (ce qui veut dire que les termes un s’approchent de plus en plus de 2 lorsque n croît). Pourtant si on calcule ces termes sur n’importe quel ordinateur (sauf avec un système qui fait du calcul exact avec des nombres rationnels), on aura l’impression qu’elle tend vers 2000.
Par exemple, la table suivante montre ce qu’on obtient avec une arithmétique virgule flottante de base 10 avec une précision de 10 chiffres (comme celle d’une calculette, par exemple).
| n | Valeur calculée | Valeur exacte arrondie |
| 2 | 1,800001 | 1,800000000 |
| 3 | 1,890000 | 1,888888889 |
| 4 | 3,116924 | 1,941176471 |
| 5 | 756,3870306 | 1,969696970 |
| 6 | 1996,761549 | 1,984615385 |
| 7 | 1999,996781 | 1,992248062 |
| 8 | 1999,999997 | 1,996108949 |
| 9 | 2000,000000 | 1,998050682 |
| 10 | 2000,000000 | 1,999024390 |
Comment faire dès lors pour s’assurer que le signe du résultat n’est pas affecté ?
Une solution s’impose : demander à l’ordinateur de faire le travail pour nous ! Une manière de procéder est de faire appel à l’arithmétique d’intervalles. Son principe est de remplacer toute valeur x par un intervalle [x,x] qui exprime l’incertitude qu’on a sur celle-ci. Par exemple, √2 pourrait être remplacé par [1,41; 1,42] qui contient la valeur exacte de √2. Toutes les opérations ( , –, sin…) sont redéfinies pour agir sur des intervalles. La garantie est la suivante : si f ([x,x]) désigne l’intervalle calculé avec ces nouvelles opérations à partir de [x,x], on est sûr qu’il contient la valeur exacte de f(x).
Tout au long des calculs, le programme élargit si nécessaire les intervalles pour qu’ils incluent les erreurs d’arrondi. On perd en précision mais on gagne l’absolue certitude que le résultat exact f(x) se situe entre les bornes de l’intervalle final f ([x,x]). Cette estimation (par défaut et par excès) de f(x) est donc exacte malgré les calculs arrondis exécutés par le programme. Ainsi le résultat satisfait les standards de rigueur mathématique et peut par conséquent être utilisé comme ingrédient d’une preuve.
Dans le cas qui nous occupe, il suffit de prendre des intervalles [a,a] et [b,b] qui contiennent a et b. Si f ([a,a]) et f ([b,b]) ne contiennent pas 0, alors on connaît le signe de f(a) et f(b) avec certitude et le théorème des valeurs intermédiaires nous garantit l’existence d’une racine.
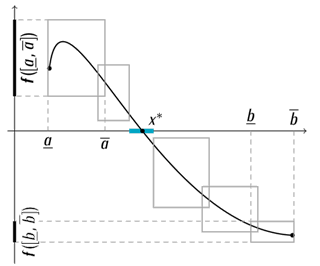
Évaluation d’une fonction grâce à l’arithmétique d’intervalles.
Remarquons que l’évaluation de f sur d’autres intervalles permet de localiser la racine x*. Ceci est illustré sur la figure ci-contre où on est certain que x* appartient au petit intervalle bleu. Un théorème affirme que, si la dérivée de f ne s’annule pas sur cet intervalle, la racine est unique. À nouveau, l’arithmétique d’intervalles permet à un ordinateur de vérifier l’hypothèse de ce théorème.
Les techniques que nous venons d’esquisser (théorèmes mathématiques combinés avec des estimations rigoureuses faites par ordinateur) forment la base des preuves assistées par ordinateur en analyse mathématique. Celles-ci sont actuellement en plein essor.

Attracteur de Lorenz.
Comme exemple particulièrement intéressant, citons le système d’équations de Lorenz qui est un modèle très simplifié de la dynamique atmosphérique. (Voir sur Interstices : L’effet papillon n’existe plus !). En 1998, Z. Galias et P. Zgliczynski ont démontré, à l’aide de l’ordinateur, que ce système exhibe un comportement chaotique. Son comportement à long terme, reflété par son attracteur, a été inclus dans la liste de 18 problèmes difficiles pour le 21e siècle proposée par S. Smale, médaillé Fields. En 2002, W. Tucker a résolu ce problème en montrant, au moyen d’une preuve assistée par ordinateur, que l’attracteur de Lorenz possède une dimension non-entière.
Mentionnons que ces méthodes sont aussi utilisées par l’équipe d’Analyse Numérique de l’UMONS pour étudier les propriétés qualitatives (en particulier les symétries) des solutions d’équations aux dérivées partielles. Ces recherches sont réalisées en collaboration avec l’Université du Connecticut et avec le soutien du Fonds de la Recherche Scientifique – FNRS, dédié au financement de projets de recherche en Belgique.
Ces exemples de preuves par ordinateur de types très différents, qui concernent des communautés de chercheurs très différentes, illustrent bien à quel point l’ordinateur est devenu pour les mathématiciens un outil non pas simplement de calcul, mais contribuant véritablement au processus de découverte.
- K. Appel, W. Haken, Every planar map is four colourable, Contemporary Mathematics 98 (1989)
- N. Robertson, D. Sanders, P. Seymour, R. Thomas, The Four-Colour Theorem, Journal of Combinatorial Theory, Series B, 70 (1997), pp. 2–44
- G. Gonthier, A computer-checked proof of the Four Color Theorem
- H. Mélot, Facet defining inequalities among graph invariants: The system GraPHedron, Elsevier Discrete Applied Mathematics 156 (2008) 1875 – 1891
- P. Turán, Eine Extremalaufgabe aus der Graphentheorie, « On an extremal problem in graph theory », Matematikai és Fizikai Lapok 48 (1941) 436 – 452
- O. Ore, Theory of Graphs, American Mathematical Society, Providence (1962)
- J. Christophe, S. Dewez, J.-P. Doignon, S. Elloumi, G. Fasbender, P. Grégoire, D. Huygens, M. Labbé, H. Mélot, H. Yaman, Linear inequalities among graph invariants: using GraPHedron to uncover optimal relationships, Networks 52 (2008) 287 – 298
- Z. Galias, P. Zgliczynski, Computer assisted proof of chaos in the Lorenz system, Physica D, 115, 165-188 (1998)
- W. Tucker, A Rigorous ODE Solver and Smale’s 14th Problem, Foundations of Computational Mathematics (2002) 2:53–117
Une première version de ce document est parue dans le magazine « élément » de l’Université de Mons, n°05, en mars 2011.
Newsletter
Le responsable de ce traitement est Inria. En saisissant votre adresse mail, vous consentez à recevoir chaque mois une sélection d'articles et à ce que vos données soient collectées et stockées comme décrit dans notre politique de confidentialité
Niveau de lecture
Aidez-nous à évaluer le niveau de lecture de ce document.
Votre choix a été pris en compte. Merci d'avoir estimé le niveau de ce document !

Hadrien Mélot

Christophe Troestler