Manipulation informatique des objets géométriques

Comment représenter ces objets ? Avec des nombres qui caractérisent leur taille, leur forme, etc. Pour un nombre entier ou rationnel, la représentation informatique est facile. Pour un nombre réel, c’est déjà beaucoup plus difficile. Le lien entre géométrie et nombre est fort : rappelons par exemple que c’est un problème géometrique, déterminer la diagonale du carré, qui a montré aux Pythagoriciens qu’il existait des nombres irrationnels.

Manœuvres d’approche

La représentation d’une surface, à condition de connaître son équation avec des coefficients qui sont des nombres représentables, est également facile. Mais la plupart des objets géométriques ne se laissent pas représenter par une équation, et on ne peut les appréhender que comme assemblages de surfaces ou de volumes élémentaires représentables mathématiquement et informatiquement. En général, il faut beaucoup d’objets élémentaires pour représenter un objet réel : une molécule peut être composée de dizaines de milliers d’atomes, une pièce mécanique d’un grand nombre de facettes.

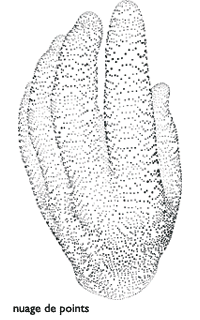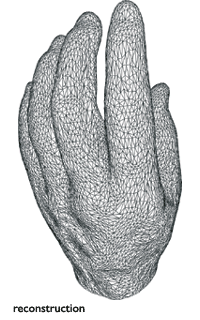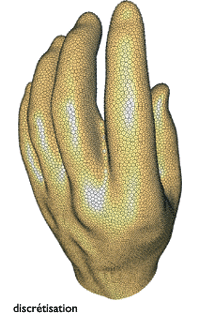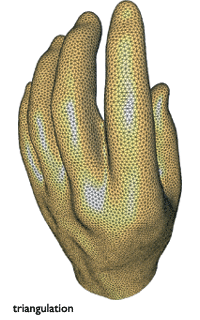
Les différentes étapes de la modélisation de la main.

Un environnement naturel ne pourra être qu’approché par un grand nombre de primitives simples. L’objet géométrique est alors composé à la fois d’un ensemble d’objets élémentaires (des facettes triangulaires par exemple) et d’une structure combinatoire donnant les relations d’incidence entre ces objets élémentaires. Trouver les bonnes structures combinatoires et les algorithmes efficaces pour les manipuler est au cœur de la géométrie algorithmique.

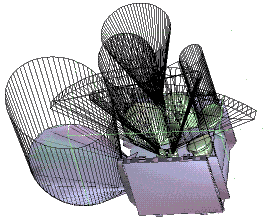
Placement géométrique des antennes d’un satellite.

Pour aménager l’espace

Un problème typique récurrent, utilisant ces fondements, concerne l’aménagement optimal de l’espace. On peut ainsi définir un algorithme permettant de disposer au mieux des antennes dans le volume restreint d’un satellite de télécommunications, en tenant compte de leur encombrement et en évitant les interférences dues au recouvrement de leurs zones d’émission.

Pour reconstruire un objet

D’autres problèmes pratiques relèvent de la reconstruction de surface ou de volume à partir d’un ensemble de points. L’idée est de disposer d’un modèle 3D d’une maquette ou d’un objet qu’on a devant soi, afin de pouvoir le manipuler sur ordinateur, l’agrandir, l’observer sous tous les angles, le modifier à loisir, l’envoyer par Internet, etc.

Il faut déterminer les points de l’objet dont on a besoin de connaître la position précise, pour interpoler géométriquement le reste de l’objet. La mesure de ces points peut s’effectuer à l’aide de capteurs disposés sur l’objet, ou par des techniques de scanner. Il faut alors trouver une triangulation (ou maillage) qui relie ces points en une structure 3D cohérente, pour construire un objet géométrique décrivant convenablement l’objet initial. L’algorithmique intervient pour reconstruire de manière systématique et efficace l’objet désiré.

Un tel outil de reconstruction peut servir dans des domaines aussi divers qu’inattendus.

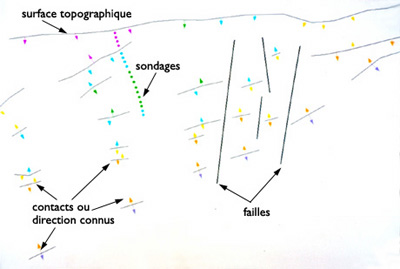
De la coupe géologique…	…à la reconstruction volumique de terrain.

Pour le tracé d’un tunnel sous les Alpes, un algorithme géométrique a permis d’obtenir un modèle raisonnable du sous-sol et des zones à éviter, à partir d’un nombre réduit de sondages, qui sont très onéreux.

En médecine, la constitution de modèles 3D d’organes ou du squelette d’un patient à partir de quelques points offre des avantages considérables.

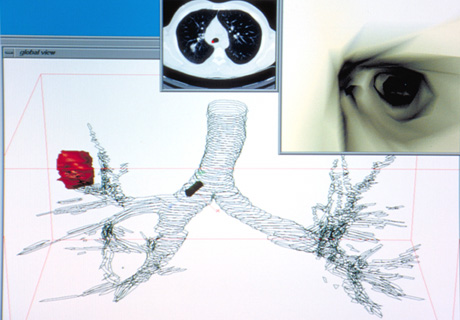
Simulation d’une endoscopie.

Un tel modèle peut en particulier être transmis sur Internet, pour une analyse, voire une manipulation à distance par un chirurgien.

Des applications plus quotidiennes encore des algorithmes géométriques concernent la vente par correspondance de prêt-à-porter, d’outils, ou de meubles sur mesure, que l’on peut positionner virtuellement dans un modèle de son appartement.

Pour transmettre des données

Compression géométrique de maillages.

De manière générale, sur Internet, entre les entreprises, ou avec les clients, on partage de moins en moins des images des objets sur lesquels on travaille, qui sont par nature figées, mais plutôt des modèles géométriques 3D, que chacun peut manipuler à sa guise. Si les objets sont représentés de manière astucieuse, des algorithmes de compression des données géométriques peuvent alors apporter d’importants gains de temps lors des transmissions électroniques, et de volume pour le stockage.