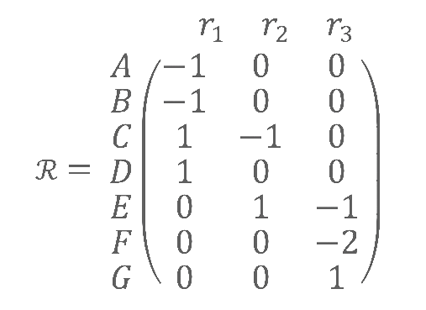
Modéliser les communautés bactériennes pour mieux comprendre leur fonctionnement

Les microbiotes sont des ensembles de micro-organismes vivant dans un environnement donné, comme par exemple l’intestin humain, l’environnement racinaire des plantes ou l’océan. Ces communautés sont des écosystèmes extrêmement complexes, comportant des milliards de microbes issus de centaines d’espèces différentes, interagissant ensemble et avec leur environnement. Les microbiotes fournissent d’innombrables services : conservation et transformation des aliments, stimulation de l’immunité, protection contre des infections, protection des cultures, captation de carbone… Bien souvent, les microbes pris isolément sont incapables de rendre seuls le service attendu. Ce sont les interactions entre microbes de la communauté qui permettent de faire émerger à l’échelle de la communauté ces fonctions d’intérêt. Il est donc important de mieux comprendre ces interactions pour espérer bénéficier des services rendus par les microbes : il faut dans un premier temps étudier individuellement chaque microbe, puis décrypter leurs interactions afin d’espérer prédire ou piloter les fonctions de la communauté. Chaque échelle d’étude recèle ses propres défis informatiques ou mathématiques.

Étudier les microbes à partir de leurs séquences d’ADN

Pour mieux comprendre les rôles des différents microbes dans leur écosystème, il est nécessaire d’avoir accès aux séquences d’ADN de chacun des membres, et pour cela, les progrès technologiques liés au séquençage ont été déterminants. Lors de l’étude d’un échantillon de microbiote, l’ensemble du matériel génétique de la communauté, initialement dupliqué dans les cellules, est fractionné et mélangé : des centaines de milliers de fragments sont choisis aléatoirement dans cette soupe pour être séquencés. Le métagénome est l’ensemble des séquences d’ADN aussi appelées lectures ou reads, résultant du séquençage ; elles sont chevauchantes, plus ou moins longues et plus ou moins sujettes aux erreurs selon les technologies. Les lectures doivent passer par une étape d’assemblage qui permettra de reconstruire le génome des espèces en présence, c’est-à-dire de grouper et ordonner les séquences en se basant sur leurs chevauchements afin d’obtenir la molécule d’ADN complète de chaque espèce.

Pour un unique organisme séquencé, cette étape s’apparente à la reconstruction d’un puzzle ; pour un microbiote, il s’agit donc de reconstruire jusqu’à des milliers de puzzles de millions de pièces, toutes mélangées. Cette étape est cruciale pour la suite des analyses et nécessite des algorithmes bioinformatiques efficaces pour passer à l’échelle de données massives et reconstruire des génomes de qualité. Décoder le génome et les gènes qui le composent permet ensuite d’inférer quelles sont les fonctions portées par les organismes dans leur écosystème, c’est-à-dire quelles transformations de biomolécules les cellules peuvent réaliser. Il s’agit ensuite d’organiser cette connaissance et de la représenter sous une forme exploitable. C’est l’objet d’étude du métabolisme, qui est représenté sous forme de réseaux en bioinformatique.

Les réseaux métaboliques pour modéliser les fonctions de chaque organisme

Le génome contient une multitude d’informations déterminant le fonctionnement de la cellule. Parmi celles-ci se trouvent les gènes qui codent pour des protéines qui peuvent réaliser des fonctions dans la cellule. Ces dernières peuvent être représentées sous la forme de réactions biochimiques telles que :

\[ 1A + 1B \overset{r_1}{\rightarrow} 1C + 1D \]

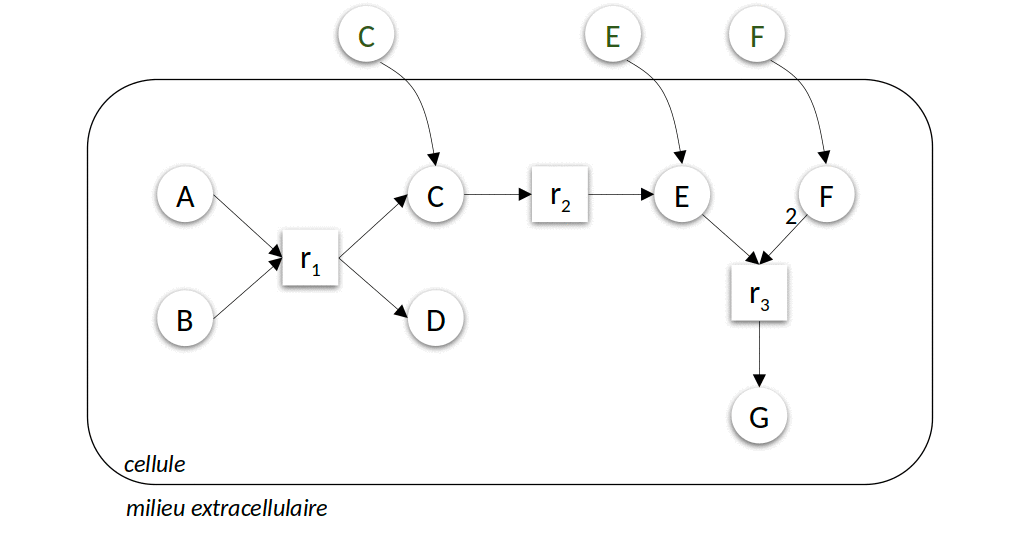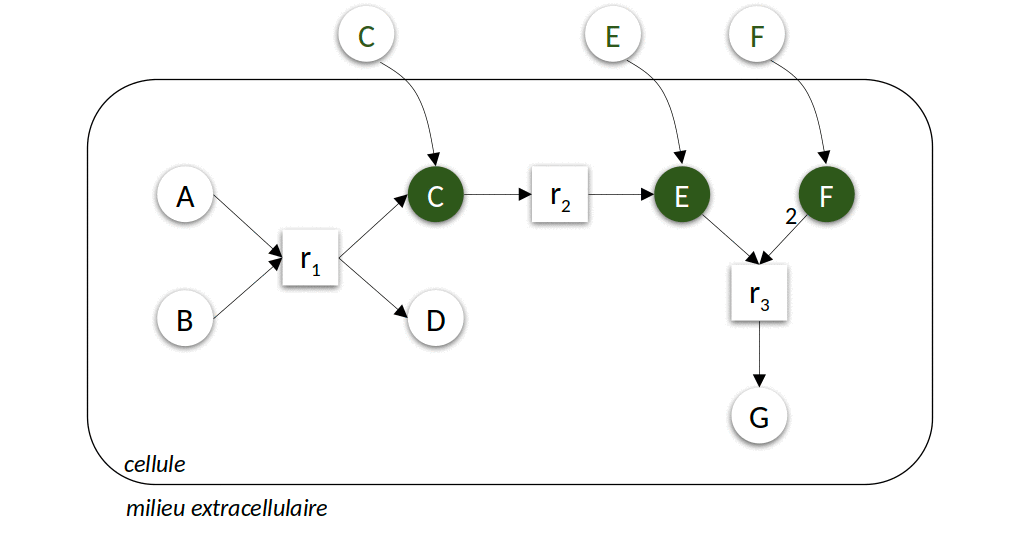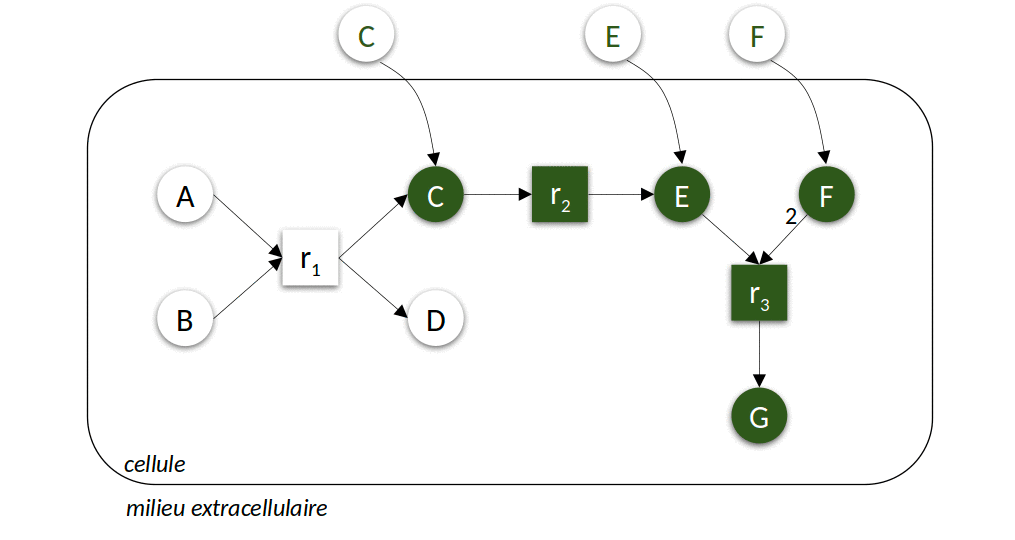
Dans cet exemple, \(A\) et \(B\) sont des molécules constituant les substrats de la réaction, qui sont transformées en produits \(C\) et \(D\) par l’activité enzymatique de la protéine associée à la réaction \(r_1\). Les nombres associés à chaque molécule sont les coefficients stœchiométriques et indiquent le nombre de molécules impliquées dans la réaction. Des bases de données et des outils d’annotation permettent de trouver les gènes de tout un génome et de leur associer une fonction, formant des ensembles de réactions que l’on appelle réseaux métaboliques. Nous ne donnerons pas de détails sur le processus de reconstruction, pour nous focaliser sur les modèles constructibles à partir des réseaux obtenus. La figure 1 montre un petit réseau métabolique, constitué de 3 réactions, dont la réaction \(r_1\) et impliquant 7 molécules.

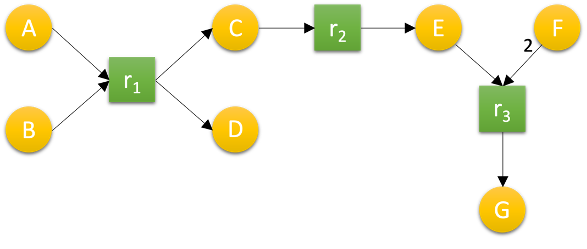
Figure 1 : Un exemple de réseau métabolique.
Les nœuds \(r_1\), \(r_2\) et \(r_3\) (nœuds carrés) sont des réactions métaboliques, \(A\), \(B\), \(C\), \(D\), \(E\), \(F\) et \(G\) (nœuds ronds) sont des molécules. Les flèches entrantes dans un nœud réaction dénotent une relation de consommation, les flèches sortantes une relation de production. L’étiquetage des flèches symbolise le nombre de molécules impliquées dans la relation, l’absence d’annotation signifiant 1 par défaut. Ainsi, la réaction \(r_3\) consomme une molécule de \(E\) et deux molécules de \(F\) pour produire une molécule de \(G\).

Un réseau métabolique à l’échelle génomique, c’est-à-dire contenant l’ensemble des réactions associées aux protéines présentes dans le génome d’un seul organisme, contient généralement plusieurs milliers de réactions. Pour une communauté microbienne, on peut donc reconstruire un réseau métabolique par génome et étudier les fonctions portées par ces espèces. L’étude des réseaux métaboliques peut utiliser une représentation sous forme de graphe (voir la Figure 1 ci-dessus), dont la visualisation est moins aisée à l’échelle d’un génome. Mais il est également commun de représenter l’information sous forme mathématique, à l’aide d’une matrice stœchiométrique \(R\) qui représente le nombre de molécules de chaque type consommées (valeurs négatives) et produites (valeurs positives) dans chaque réaction :

Ces matrices et ces graphes peuvent ensuite être associés à des modèles mathématiques, mais aussi à des données supplémentaires afin de simuler le comportement métabolique des microbes.

Utiliser les réseaux pour prédire le métabolisme

La modélisation du métabolisme consiste à prédire l’activité des réactions d’un réseau, qui varie selon le contexte environnemental. En effet, plusieurs limites sont à prendre en compte lorsqu’on étudie un réseau métabolique. La première est que la présence d’un gène dans le génome ne garantit pas l’expression de la protéine associée, ni son activité. Pour savoir si une fonction est réellement activée, il faut davantage de données expérimentales analysant les processus cellulaires : transcriptomique (gènes exprimés), protéomique (protéines et enzymes présentes), métabolomiques (molécules présentes). Ces données, connues sous le nom de données « omiques », peuvent être intégrées dans les modèles métaboliques pour améliorer les prédictions. La seconde limite est que le comportement d’un microbe est déterminé par son environnement, et notamment par la composition nutritionnelle de celui-ci. Ainsi, un même réseau donnera des simulations d’activité différentes selon l’environnement modélisé.

Prédire les métabolites productibles

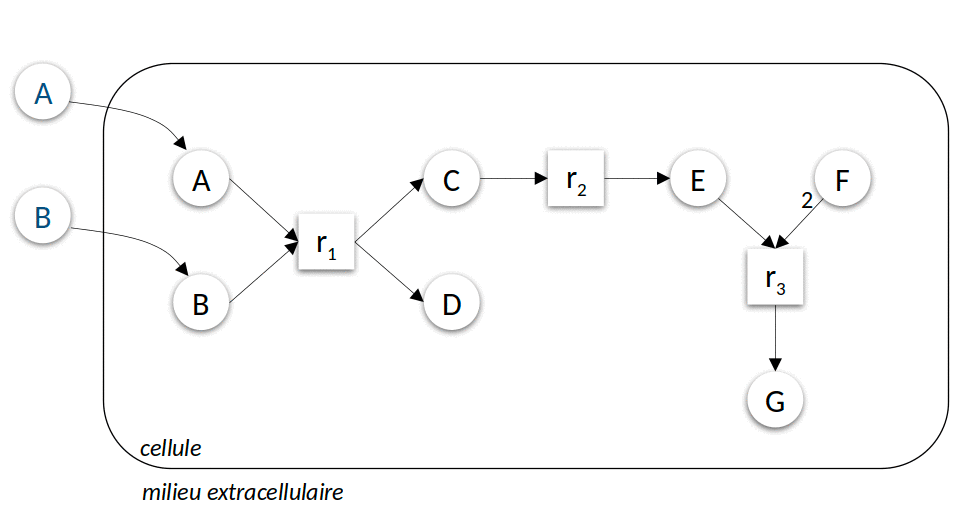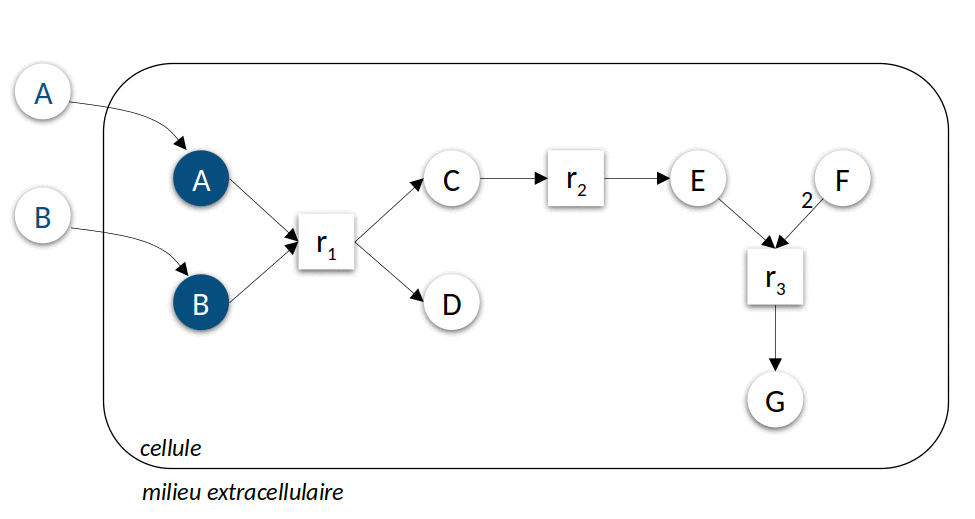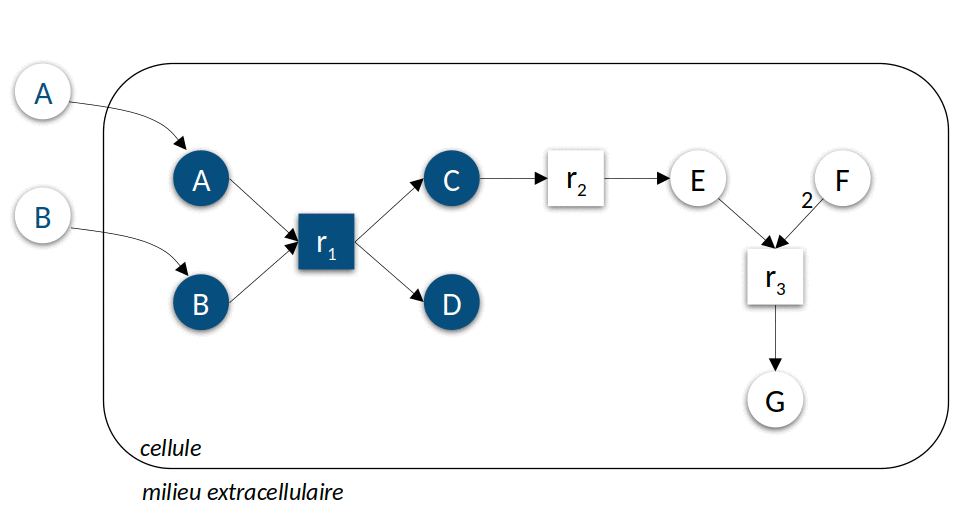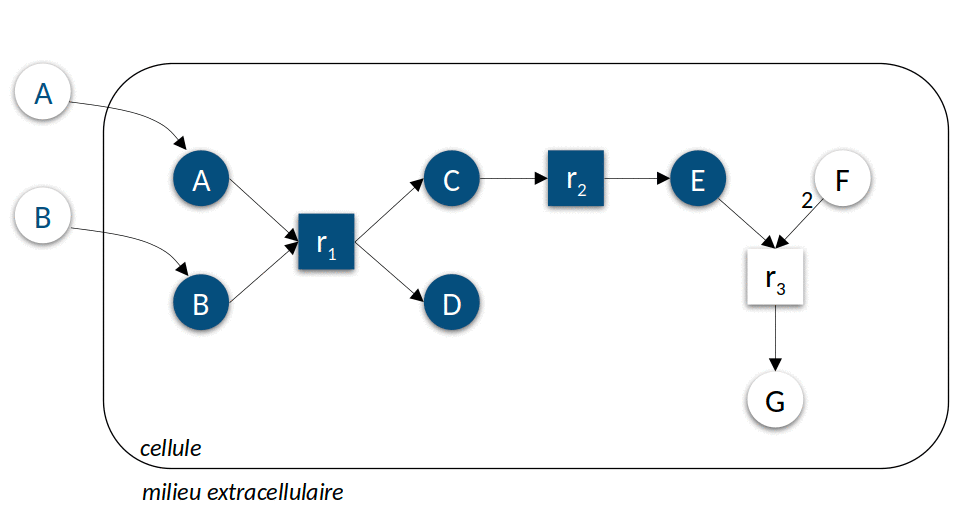
Une première modélisation du métabolisme consiste à considérer qu’une réaction est soit activée soit éteinte, et qu’un composé est soit productible soit non productible. C’est une représentation booléenne (\(0 =\) éteint / \(1 =\) allumé) de l’activation du métabolisme. L’algorithme associé à ce modèle discret est simple : à partir de composés disponibles dans le milieu, on cherche l’ensemble des composés accessibles sous l’hypothèse que les produits d’une réaction sont productibles dès lors que tous les substrats de cette réaction sont eux-mêmes productibles. Dans ce modèle, les coefficients stœchiométriques des réactions sont ignorés. Dans la réaction \(r_3\), ce modèle se contentera donc de vérifier que \(E\) et \(F\) sont productibles pour prédire la productibilité de \(G\), peu importe leurs quantités respectives.

La Figure 3 ci-dessous présente l’application itérative de l’algorithme pour prédire les ensembles des composés productibles à partir de deux sources de nutriments différentes. Cet algorithme simple peut être calculé très efficacement, permettant de l’utiliser comme modèle d’activité lors de la résolution de problèmes hautement combinatoires comme par exemple la sélection de sous-communautés d’intérêt à partir d’une communauté microbienne. Leur résolution s’appuie sur un langage de programmation spécifique à ces problèmes de raisonnement, la programmation par ensemble de réponse (Answer set programming ou ASP).

Figure 3 : Modélisation discrète du métabolisme. Dans le premier exemple (à gauche), le milieu environnemental contient les composés \(A\) et \(B\), dans le second exemple (à droite) \(C\), \(E\) et \(F\). L’animation représente les différentes itérations de l’algorithme de recherche des réactions activées et molécules produites jusqu’à l’atteinte d’un point fixe, c’est-à-dire l’impossibilité d’activer davantage de réactions.

Prédire les quantités de métabolites produits

Une seconde modélisation du métabolisme vise à prédire une valeur d’activité à chacune des réactions métaboliques. Il s’agit d’évaluer les flux métaboliques, c’est-à-dire la quantité de molécules produites ou consommées par chaque réaction par unité de temps. Une hypothèse de stationnarité est utilisée afin d’établir des relations entre les flux de chaque réaction du réseau : par exemple, pour que la concentration du métabolite \(C\) reste stationnaire à l’intérieur de la cellule microbienne, il faut que \(C\) soit consommé par la réaction \(r2\) au même taux qu’il est produit par la réaction \(r_1\). Autrement dit, le flux \(v_1\) associé à la réaction \(r_1\) doit être égal au flux \(v_2\) de la réaction \(r_2\). Cette approche pourrait s’étendre à l’ensemble des réactions du réseau en utilisant la matrice de stœchiométrie \(R\) pour résoudre un système linéaire calculant la distribution des flux (voir Figure 4). Toutefois, comme il y a plus de réactions (et donc de colonnes dans la matrice \(R\)) que de métabolites (i.e. de lignes dans \(R\)) dans les réseaux métaboliques microbiens typiques, ce système linéaire est dit « sous-déterminé ». Il faut donc faire des hypothèses supplémentaires pour contraindre ce système d’équation.

Un premier type de contraintes consiste à définir des limites pour les flux entrant et sortant du réseau, correspondant aux limites physiques des transporteurs de la cellule microbienne lui permettant d’absorber ou rejeter des métabolites. Un deuxième type de contraintes prend en compte la thermodynamique, c’est-à-dire l’énergie nécessaire pour exécuter les réactions. Dans le réseau métabolique, certaines réactions sont « productrices » d’énergie, en ce sens qu’elles dégradent les nutriments présents dans le milieu pour obtenir de petites molécules et de l’énergie. On parle de réactions cataboliques. Ces petites molécules sont recombinées par d’autres réactions « consommatrices » d’énergie, dites anaboliques, pour produire les ingrédients nécessaires à la constitution de biomasse. Certaines réactions sont réversibles, ce qui signifie qu’elles peuvent parfois dégrader, parfois recomposer des molécules plus larges. Le sens des réactions est pris en compte en imposant des bornes minimales et maximales à leurs flux respectifs. Enfin, une contrainte de minimisation ou de maximisation est ajoutée sur une ou plusieurs réactions du réseau métabolique, c’est la fonction objectif. Généralement, nous supposons que les microbes vont chercher à maximiser la biomasse produite, ce qui permet d’écrire le problème de répartition des flux dans le réseau comme un problème d’optimisation. Rajoutons une réaction de biomasse bio à notre réseau exemple, ainsi que des réactions permettant d’apporter les nutriments \(A\), \(B\) et \(F\), et enfin une réaction exportant le produit de la biomasse \(H\) (voir Figure 4). On obtient le système d’équations suivant, correspondant au modèle du Flux Balance Analysis (ou FBA par la suite), une méthode mathématique permettant de prédire les flux métaboliques (représentés ici par la variable \(v\)) dans le réseau métabolique à l’échelle du génome :

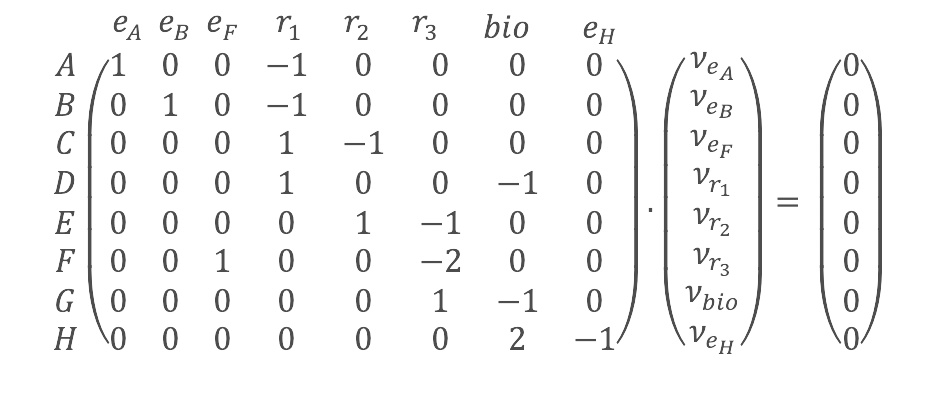
On souhaite trouver \(\nu = ( \nu_{e_A}, \nu_{e_B}, \nu_{e_F}, \nu_{r_1}, \nu_{r_2}, \nu_{r_3}, \nu_{bio}, \nu_{e_H}) \) tel que $$ \left\{ \begin{array}{c} \nu_{bio} = \max ⁡\nu_{bio} \\ b_{min} \leq \nu_{e_A} \leq b_{max} \\ b_{min} \leq \nu_{e_B} \leq b_{max} \\ b_{min} \leq \nu_{e_F} \leq b_{max} \\ \vdots \\ R.\nu=0 \end{array} \right. $$ 

D’un point de vue mathématique, ce problème est un modèle d’optimisation dit de programmation linéaire (Linear programming problem), pour lequel des algorithmes de résolution efficaces sont disponibles, permettant de résoudre des problèmes FBA à plusieurs milliers d’inconnues, correspondant aux flux des réactions composant les réseaux métaboliques.

Une solution de distribution des flux est illustrée dans la Figure 4 à travers l’épaisseur des flèches : le système d’équations et les contraintes sont respectées si les valeurs de flux de la réaction d’import de \(F\) et de la réaction d’export de \(H\) sont le double des valeurs des autres flux du réseau. Là encore, la taille des réseaux métaboliques bactériens complexifie la formalisation, l’interprétation et l’intégration de données de ces modèles mathématiques.

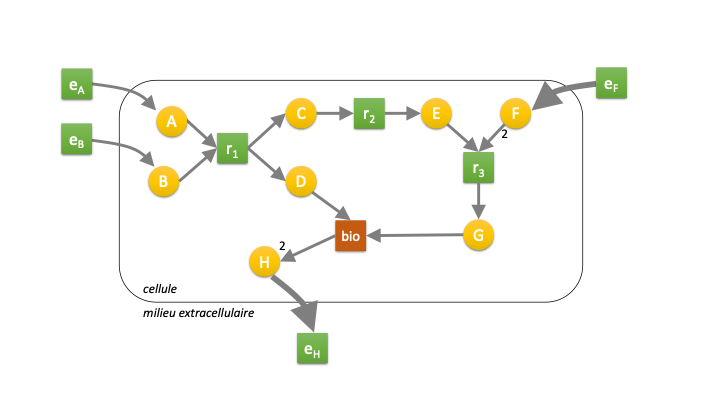
Figure 4 : Illustration d’un résultat de calcul de flux métabolique.
Dans cet exemple, les réactions \(e_A\), \(e_B\) et \(e_F\) permettent de faire rentrer des molécules dans la cellule, la réaction \(e_H\) permettant de les exporter à l’extérieur. L’épaisseur des flèches est proportionnelle aux flux calculés.

Extension des modèles individuels aux communautés microbiennes

Les modélisations ci-dessus peuvent non seulement être appliquées à des organismes individuels, mais également à des communautés d’organismes, chacun représenté par son réseau métabolique. Les modélisations communautaires prennent en compte que chaque organisme va pouvoir modifier le milieu environnemental avec les produits de son métabolisme permettant ainsi aux espèces voisines de bénéficier de ces molécules et d’activer de nouvelles réactions. De la même manière, les modèles numériques vont tenir compte de la limitation de la quantité de certaines molécules dans l’environnement et vont ainsi mettre en évidence des phénomènes de compétition pour ces substrats limitants. La prise en compte de ces interactions permet de modéliser le fonctionnement de la communauté dans son ensemble.

Une autre extension de l’approche consiste à appliquer le FBA pour étudier la dynamique du métabolisme des organismes. Dans ce cas, il faut résoudre le problème d’optimisation précédent à chaque « pas de temps » en prenant en compte le changement des conditions environnementales engendré par la consommation de nutriments et la production de métabolites à l’itération précédente. Il est ainsi possible de prédire la croissance de chaque bactérie de la communauté microbienne et l’évolution de leur environnement au cours du temps. Bien sûr, cette application vient avec ses contraintes de passage à l’échelle, et motive le développement d’approximations s’affranchissant de l’optimisation pour gagner en temps de calcul.

Des modèles pour de nouvelles applications

Les modèles communautaires offrent des perspectives nouvelles pour de nombreuses applications liées aux différents écosystèmes microbiens. En santé, des modifications de la composition du microbiote intestinal ont été mises en évidence dans de nombreuses pathologies, comme par exemple des maladies inflammatoires de l’intestin. En agro-écologie, certains micro-organismes sont associés à la protection des plantes contre des pathogènes. Dans l’océan, les micro-organismes jouent un rôle important dans le cycle du carbone, une thématique d’intérêt dans le contexte du changement climatique. Dans toutes ces applications, les mécanismes précis ne sont pas encore bien compris. Les modèles nous aident à mieux comprendre le fonctionnement de ces communautés microbiennes : de nouvelles pratiques permettant de renforcer les services rendus par les bactéries pourraient ainsi voir le jour.