Modéliser les robots à câbles

Les joueurs de pétanque (en particulier quand ils arrivent à un âge qui leur confère sagesse et rhumatismes) ne se baissent pas toujours pour ramasser les boules. Ils utilisent un aimant, pendu à une ficelle. Ce dispositif permet d’accrocher la boule et de la hisser jusqu’à hauteur de main (ce qui est bien le but). Mais sauriez-vous aller plus loin avec cette ficelle et cet aimant ? Pourriez-vous déplacer la boule de quelques mètres et la stopper net au dessus d’un point précis (sans qu’elle balance) ? Sauriez-vous l’orienter de sorte que la marque soit face à vous à son arrivée ?

Robot à câbles. © Photo : Inria.

Bien entendu, cela n’aurait pas grand intérêt pour une partie de pétanque, mais quittons cet univers détendu et intéressons-nous à des contextes plus délicats. Dans bien des situations, pour déplacer délicatement un objet lourd ou une personne, il est très utile de pouvoir contrôler avec précision l’orientation et la translation. Cela pourrait se faire avec un robot humanoïde ou un bras manipulateur comme dans les usines automobiles, mais la puissance nécessaire pour manipuler la charge conduirait à des systèmes de très grande taille et consommant beaucoup d’énergie. Pour rendre le système beaucoup plus discret et moins énergivore, on préfère utiliser plusieurs câbles dont on pilote l’enroulement par ordinateur : c’est le principe des robots parallèles à câbles, dont le document Interstices Robots et marionnettes montre des exemples concrets. La charge est ainsi répartie et peut être positionnée plus précisément.

Positionner une charge

Commençons par un exemple simple : supposons que l’on veuille déplacer une charge dans un plan vertical avec deux câbles. Pour cela, on doit pouvoir calculer les longueurs des deux câbles pour mettre la charge dans une position connue. Les roboticiens appellent cela résoudre le modèle géométrique inverse. Eh bien, nous avons de la chance, car cela se fait très bien ! Pour le comprendre, utilisez l’applet suivante.

Pour accéder à l’applet Java, autorisez les applets du domaine https://interstices.info. Si votre navigateur n’accepte plus le plug-in Java, mais que Java est installé sur votre ordinateur, vous pouvez télécharger le fichier JNLP, enregistrez-le avant de l’ouvrir avec Java Web Start.

Deux treuils, placés en P1 et P2, peuvent enrouler ou dérouler deux câbles reliés à une masse de 50 kilogrammes (le rectangle noir). Pour déplacer la masse, cliquez dessus avec le bouton gauche de la souris en le maintenant appuyé. Pour chaque position où vous allez mettre la masse, l’applet va vous indiquer la longueur des câbles pour cette position, ainsi que la tension dans les câbles (vous remarquerez que cette tension est en général bien inférieure à 50, ce qui signifie qu’on a bien réparti la charge sur les deux câbles).

Cette applet permet aussi de mettre en évidence des limitations de ce type de robot. La première question que l’on peut se poser est de délimiter la zone où l’on peut placer la charge. Pour cela :

• déplacez la charge d’abord latéralement : si les câbles disparaissent, c’est que la position de la charge n’est pas atteignable ;
• ensuite, placez la charge au milieu et faites-la monter progressivement, tout en observant la valeur des tensions dans les câbles. Cette tension est limitée à 100, au-delà, le câble casse. Que se passe-t-il si l’on monte trop haut ?
• plus subtil : est-ce que les deux câbles du robot sont toujours tendus ? La réponse est non : il existe des positions de la charge où un seul câble est en tension, le deuxième câble pendant. Essayez de les trouver.

Déterminer les longueurs des câbles

Nous n’avons pas expliqué comment on obtenait la solution du modèle géométrique inverse, mais peut-être l’avez-vous deviné ? Alors, vous êtes prêt à jouer au jeu suivant.

Observez bien la figure suivante. À partir des coordonnées des points de fixation des treuils et de la position de la charge, pouvez-vous calculer la longueur des câbles ? Vous avez sans doute appris en classe la formule de géométrie qui s’applique ici…

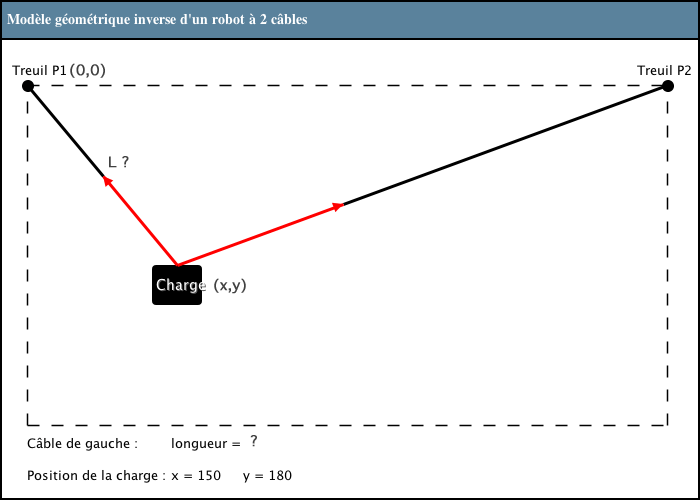
Comment calculer la longueur du câble de gauche ? Pour obtenir un indice, cliquez sur l’image.

Le bon équilibre

Pour le moment, nous avons la vie belle : puisque l’on sait quelles doivent être les longueurs des câbles pour mettre la charge à une position donnée, il est très facile de commander ce robot. Pour atteindre une position donnée, il suffit de calculer les longueurs et d’envoyer ces informations aux treuils, munis d’un système de contrôle qui va enrouler ou dérouler les câbles pour les mettre à la longueur voulue.

Mais dans notre expérience précédente, nous avons vu qu’il existe des positions de la charge pour lesquelles seule la longueur d’un câble est importante, l’autre pouvant avoir n’importe quelle valeur, du moment qu’elle est plus grande que la distance entre la charge et le point P.

Ce cas particulier est dû au fait qu’avec un câble, il est possible de tirer, mais non de pousser une charge. C’est la grande différence entre les robots parallèles à câbles et leurs frères à jambes rigides. Or la charge est soumise à une loi physique, elle doit être en équilibre mécanique : la somme des forces auxquelles elle est soumise doit être nulle. Faisons un bilan de ces forces. Nous avons

• la gravité, qui s’applique selon la verticale vers le bas
• les tensions dans les câbles, qui sont dirigées selon la direction des câbles s’ils sont en tension. Si la longueur d’un câble attaché à un point Pi est plus grande que la distance entre Pi et la charge, alors sa tension est nulle

Mathématiquement, l’équilibre s’écrit
\[-mg \vec{z} +\tau_1 \vec{n_1} + \tau_2 \vec{n_2} = 0 \:\: (1)\]
où \(\tau_1\), \(\tau_2\) sont les tensions dans les câbles
et \(\vec{n_1}\), \(\vec{n_2}\) les vecteurs unitaires qui donnent la direction des câbles.

On peut aussi écrire cette relation sous la forme matricielle :
\[ J \left( \begin{array}{c} \tau_1 \\ \tau_2 \end{array} \right) = \left( \begin{array}{c} 0 \\ mg \end{array} \right) \:\: (2) \]
où \(J\) a comme colonnes \(\vec{n_1}\) et \(\vec{n_2}\).
On peut aussi l’écrire comme :
\[ M \left( \begin{array}{rrr} \tau_1 \\ \tau_2 \\ -mg \end{array} \right) = 0 \:\: (3)\]
\[ \mbox{où } M = \left( \begin{array}{ccc} n_1^x & n_2^x & 0 \\ n_1^z & n_2^z & 1 \end{array} \right) .\]

Pour notre robot à deux câbles accrochés au même point, le modèle géométrique inverse se résout en utilisant la géométrie pour trouver la longueur des câbles. Ensuite, nous avons utilisé la relation d’équilibre (2) pour calculer les tensions dans les câbles, ce qui permet de vérifier si les câbles sont bien en tension.

Il est parfois nécessaire d’utiliser la relation d’équilibre pour résoudre le modèle géométrique inverse. Pour cet exemple, nous allons accrocher nos deux câbles en deux points différents de la charge. Au contraire du robot précédent, la charge peut maintenant non seulement se translater, mais aussi tourner. Mais comme l’on n’a que deux câbles, on ne peut pas à la fois contrôler le déplacement de la charge (selon les directions \(x\), \(y\)) et sa rotation (déterminée par exemple par l’angle \(\theta\) entre la direction de la charge et l’axe des \(x\)). On a donc trois paramètres qui déterminent la position de la charge, mais seulement deux variables de contrôle, les longueurs des deux câbles.

Pour le modèle géométrique inverse, on doit fixer la valeur de deux des trois paramètres de position de la charge. Dans l’exemple suivant, on va fixer la position en \(x\) et \(y\) de la charge, mais la longueur des câbles dépend maintenant aussi de l’orientation \(\theta\) de la charge. Pour calculer ces longueurs, les relations géométriques ne suffisent plus. C’est là qu’intervient l’équilibre mécanique : dans les trois équations (2) nous avons trois inconnues, les tensions \(\tau_1\), \(\tau_2\) et l’angle θ\(\theta\)car les vecteurs \(\vec{n_1}\), \(\vec{n_2}\) dépendent de cet angle. On peut facilement résoudre deux de ces équations en \(\tau_1\), \(\tau_2\) et reporter le résultat dans l’équation restante, qui devient une équation dans la seule inconnue \(\theta\). Sans entrer dans les détails, cette équation peut admettre plusieurs solutions en \(\theta\) et à chacune d’entre elles correspondent différentes longueurs de câbles. Le modèle géométrique inverse a donc plusieurs solutions. Dans l’applet suivante, vous pouvez fixer la position de la charge avec la souris. Le programme calcule pour vous les différents angles \(\theta\) possibles ainsi que les longueurs correspondantes des câbles.

Pour accéder à l’applet Java, autorisez les applets du domaine https://interstices.info. Si votre navigateur n’accepte plus le plug-in Java, mais que Java est installé sur votre ordinateur, vous pouvez télécharger le fichier JNLP, enregistrez-le avant de l’ouvrir avec Java Web Start.

Pour résoudre le modèle géométrique inverse, nous avons été obligés d’introduire comme inconnues \(\tau_1\), \(\tau_2\) qui, a priori, ne sont pas d’un intérêt direct, puisque l’on recherche les longueurs des câbles. Aurait-t-on pu s’en passer ? La réponse est oui, car si l’on regarde l’équilibre mécanique (3), on peut remarquer qu’il s’écrit sous la forme d’un système linéaire \(MX=0\). Ce type de système admet la solution triviale \(X=0\) (qui n’est pas admissible pour notre cas) ou ne peut être satisfait que si le déterminant de \(M\) est nul, ce qui nous fournit une équation supplémentaire. Cette équation nous permet alors de déterminer l’orientation \(\theta\).

Mais on peut encore aller plus loin : les colonnes de \(M\) caractérisent d’une part les lignes associées aux câbles et, d’autre part, la ligne verticale associée à la gravité. L’annulation du déterminant de \(M\) indique que ces colonnes sont dépendantes. Or une géométrie particulière, la géométrie de Grassmann, s’intéresse à la traduction géométrique de la dépendance linéaire entre des vecteurs qui caractérisent des lignes droites. Dans notre cas, cette géométrie indique que le seul cas où il y a dépendance entre 3 vecteurs est obtenu quand les 3 lignes se coupent au même point. Dans l’applet précédente, vous pouvez observer ce phénomène en cliquant sur le bouton Montrez les lignes qui va prolonger les lignes associées aux câbles et vous montrera en vert la ligne associée à la gravité. Vous verrez alors qu’effectivement, pour toutes les solutions, les 3 lignes se coupent au même point.

L’inverse de l’inverse

Jusqu’à présent, nous ne nous sommes intéressés qu’au modèle géométrique inverse. Mais nous allons montrer que cela n’est pas suffisant. Supposons que vous ayez des caméras qui observent le robot et qui vous permettent d’estimer les longueurs des câbles. Pouvons-nous, à partir de ces mesures, retrouver la position de la charge ? C’est ce que les roboticiens appellent résoudre le modèle géométrique direct.

Un robot parallèle à six jambes rigides : simulateur de vol de la Lufthansa.
Photo : Ethan Arnold, Wikimedia Commons CC-BY-SA.

Pour les robots parallèles à jambes rigides, le problème du modèle géométrique direct se pose aussi. Les robots de ce type ont souvent six jambes, c’est le cas par exemple des simulateurs de vol. Ce n’est pas un hasard : dans l’espace, un objet peut se déplacer dans trois directions et tourner autour de chacune de ces directions (on dit qu’il a six degrés de liberté). La pose complète d’un objet dans l’espace se caractérise donc par six paramètres. Pour les contrôler indépendamment, il faut alors au moins six jambes. Pour notre problème de modèle géométrique direct, nous avons les mesures des six longueurs des jambes, obtenues à l’aide de capteurs placés dans chacune des jambes, et nous devons en déduire la valeur des six paramètres de pose de la charge.

Il s’agit d’un problème ancien, puisque le mathématicien Cauchy l’avait abordé dès 1812, et qu’un
concours autour de ce thème avait été organisé par l’Académie des Sciences en 1900 (un des deux gagnants de ce prix avait été le mathématicien Borel). Mais bien sûr, à l’époque, l’intérêt pour ce
problème n’était que théorique, puisque la technologie disponible ne permettait pas de construire une telle machine. Ce n’est qu’après la seconde guerre mondiale que sont apparues les premières machines de ce type. En particulier, l’ingénieur Gough a développé une machine destinée à tester l’usure des pneumatiques chez Dunlop. Stewart, en 1965, proposait le premier concept de simulateur de vol.

Mais ce n’est vraiment que dans les années 80 que s’est ravivé l’intérêt pour le problème du modèle géométrique direct, avec l’espoir que les ordinateurs permettraient d’en calculer la solution. On peut résumer ce problème de la manière suivante : les 6 longueurs des jambes sont des fonctions relativement simples des 6 paramètres qui décrivent la posture de l’objet. Comme ces longueurs sont connues, il faut donc résoudre ce système de 6 équations à 6 inconnues. Au début des années 90, il a été montré qu’il n’y aurait pas plus de 40 solutions à ce problème et au milieu des années 90, il a été proposé un exemple avec effectivement 40 solutions : pour des longueurs de jambes fixées, la charge peut se trouver en 40 positions différentes ! Toutefois, ce n’est que dans les années 2000 que l’on a vu apparaître des méthodes numériques efficaces pour calculer effectivement les solutions dans un temps relativement faible (de l’ordre de quelques secondes).

Revenons maintenant aux robots à câbles et considérons l’exemple du robot à 2 câbles attachés en 2 points différents de la charge. Pour ce robot qui se déplace dans le plan, nous avons besoin de 3 paramètres pour caractériser la position de la charge (les coordonnées de son centre et l’angle \(\theta\) pour l’orientation). Si l’on écrit les longueurs des deux câbles comme fonction de ces paramètres, on n’obtient que 2 équations, ce qui est insuffisant pour calculer les trois paramètres. On est donc obligé d’utiliser aussi l’équilibre mécanique, qui va fournir l’équation manquante. Une manipulation de ces équations montre que ce système peut avoir jusqu’à 12 solutions ! Toutefois, toutes les solutions ne sont pas valides : en effet, n’oublions pas que seules les solutions avec les câbles en tension sont correctes. De plus, avoir des câbles en tension est nécessaire, mais n’est pas suffisant : une solution peut être stable ou instable (dans ce cas, à la moindre perturbation, la charge va aller vers une autre solution). Pour illustrer ce problème de stabilité, considérez une tige avec une masse à son extrémité alors que vous tenez entre deux doigts l’autre extrémité de la tige. La masse peut alors être en deux positions :

• la masse au-dessus de vos doigts, ce qui est une position hautement instable ;
• la masse au-dessous de vos doigts, qui est une position stable.

Dans un système dynamique, comme un robot, il est très rare que la charge reste dans une position instable.

On est encore loin d’avoir exploré toutes les facettes du problème du modèle géométrique direct du robot à deux câbles, pourtant le plus simple que l’on puisse imaginer. Par exemple, on ne sait pas s’il existe une géométrie de robot et des longueurs de câble pour lesquels on a effectivement 12 solutions valides, qu’elles soient stables ou instables.

Élargissons maintenant le problème, en augmentant le nombre de câbles. On peut distinguer deux catégories de robots, pour lesquels on va résoudre le modèle géométrique direct de manière différente :

• celui où le nombre de câbles est égal au nombre de paramètres qui permettent de caractériser la position de la charge,
• celui où ce nombre est inférieur au nombre de paramètres de pose.

Dans la première catégorie, on trouve par exemple :

• un robot à 3 câbles, tous attachés en des points différents sur
  la charge, qui déplace la charge dans un plan (la position de la charge est déterminée par 3 paramètres : la position \(x\), \(y\) du centre de masse et l’orientation)
• un robot à 3 câbles, tous attachés au même point, qui déplace en \(x\), \(y\), \(z\) la charge dans l’espace sans en contrôler l’orientation
• un robot à 6 câbles, tous attachés en des points différents sur la charge, qui déplace une charge dans l’espace.

Pour cette catégorie, on a affaire à un problème découplé : puisque l’on a le même nombre de paramètres de position de la charge que d’équations de longueur, on peut trouver les paramètres de pose en utilisant le modèle géométrique direct des robots parallèles à jambes rigides, bien maîtrisé. On calcule ensuite les tensions dans les câbles en résolvant (2) pour chacune des solutions, afin de retenir celles avec les câbles en tension.

Par contre, pour l’autre catégorie, cette manière de traiter le problème en deux temps ne s’applique pas. Prenons l’exemple du robot à 3 câbles, tous attachés en des points différents sur la charge, qui déplace la charge dans l’espace. Les longueurs des câbles fournissent 3 équations, mais cela n’est pas suffisant, puisque nous avons à déterminer 6 paramètres de position pour la charge. On est donc obligé de faire intervenir les 6 équations d’équilibre mécanique, ce qui impose d’introduire comme inconnues supplémentaires les 3 tensions dans les câbles. On se retrouve donc avec un système de 9 équations à 9 inconnues. Si l’on se rappelle qu’il a fallu quasiment 20 ans pour résoudre de manière satisfaisante le modèle géométrique direct du robot parallèle à jambes rigides, qui n’avait que 6 équations en 6 inconnues, on peut comprendre que ce problème soit encore non complètement résolu ! Le dernier résultat connu en 2011 indique que le nombre de solutions ne doit pas dépasser 158, mais l’on peut suspecter que ce nombre est surestimé.

Et la complexité augmente encore si l’on a plus de câbles : 10 équations à 10 inconnues pour un robot à 4 câbles et 11 équations à 11 inconnues pour un robot à 5 câbles. À l’heure actuelle, personne n’a réussi à établir un quelconque résultat pour de tels robots à 4 ou 5 câbles…

C’était trop simple !

Vous pouvez peut-être croire que ces problèmes de modèles géométriques directs sont très théoriques. Pourquoi s’intéresser au problème à 4 ou 5 câbles si l’on a sous la main un robot à 6 câbles ? Supposons que vous vouliez atteindre une certaine position de la charge avec un robot à 6 câbles. Vous allez calculer les longueurs de câbles avec le modèle géométrique inverse. Par acquit de conscience, vous allez vérifier le résultat avec le modèle géométrique direct. Supposons qu’il vous indique qu’effectivement, la seule solution est la position où vous désirez placer la charge. Fort de cette certitude, vous demandez aux treuils de mettre les câbles aux longueurs calculées et vous lâchez la charge… qui se met dans une position différente de celle désirée ! Que s’est-il passé ? Tout simplement, vous avez implicitement supposé que la position finale du robot serait telle que les 6 câbles sont en tension. Mais lorsque le robot est lâché, sa trajectoire est déterminée par les lois de la mécanique qui peuvent le conduire à une position finale où moins de 6 câbles sont en tension. Et, effectivement, dans sa position finale, vous allez constater que certains de ses câbles ne sont pas en tension. Dans certains cas, le robot peut même terminer sa course avec un seul câble en tension ! D’où l’importance de maîtriser l’ensemble des modèles géométriques directs, quel que soit le nombre de câbles de votre robot.

Mais même cette maîtrise ne sera pas suffisante pour déterminer la position courante de votre robot. Admettons que vous sachiez calculer les solutions stables de tous les robots avec un à six câbles en tension que vous pouvez construire à partir du robot initial (et nous avons vu que c’est loin d’être le cas). Vous savez alors que la position courante est une de ces solutions, mais laquelle ? L’analyse purement statique ne vous permet pas de le déterminer et une analyse dynamique sera très délicate. Une autre idée serait d’ajouter de l’information dans le système en ajoutant des capteurs dont les mesures permettraient d’écarter des solutions obtenues précédemment pour conduire finalement à une seule solution. Mais on ne sait pas actuellement ce qu’il faudrait mesurer de manière à être sûr de n’obtenir qu’une seule solution dans tous les cas de figure. Comme, de plus, les mesures sont forcément empreintes d’incertitude, il faudrait s’assurer que les calculs soient robustes vis-à-vis de ces incertitudes…

Le saut à l’élastique

Jusqu’à maintenant, nous avons fait une hypothèse sur les câbles : on a supposé que, quelles que soient les tensions auxquelles ils sont soumis, leurs longueurs restaient constantes. En fait, beaucoup de câbles (par exemple ceux utilisés dans les grues), s’allongent lorsque l’on tire dessus. Pour modéliser cet allongement, on fait souvent une supposition simple : le robot se comporte comme un ressort ou comme un élastique. Si \(l_0\)> est la longueur du câble non tendu, sa longueur \(l\) lorsqu’il est soumis à une tension \(\tau\) vérifie \(\tau = k (l-l_0)\)
d’où
\[ l = l_0 \tau / k \:\:(4) \]

La constante \(k\) est appelée la raideur du câble, qui va dépendre du matériau du câble ainsi que de ses dimensions. Si l’on a affaire à un robot à câbles élastiques, il faut alors reprendre complètement les problèmes des modèles géométriques en introduisant les équations (4) comme équations supplémentaires.

C’est ce que nous allons vous proposer dans l’applet suivante, où vous allez fixer avec la souris la position de la charge d’un robot à 3 câbles élastiques, tous connectés au même point de la charge. Remarquons tout d’abord que si les câbles ne sont pas élastiques, alors on ne peut pas calculer la tension dans les câbles en ne considérant que l’équilibre mécanique. En effet, l’équilibre ne fournit que 2 équations, alors que nous avons 3 tensions inconnues. Par contre, si les câbles sont élastiques, nous avons 6 inconnues (les 3 longueurs de câbles et les 3 tensions dans les câbles) et 5 équations, deux de l’équilibre et 3 provenant de (4). On a donc encore un choix possible. Pour illustrer ce choix, nous avons décidé de choisir la solution qui conduit au minimum de \(\tau_1^2 \tau_2^2 \tau_3^2\), l’idée étant de répartir au mieux les tensions entre les câbles. L’applet suivante va vous permettre de déplacer la charge à la souris et de visualiser les longueurs qui devront être envoyées comme consignes aux treuils, la distance entre les treuils et la charge, ainsi que la tension dans les câbles.

Pour accéder à l’applet Java, autorisez les applets du domaine https://interstices.info. Si votre navigateur n’accepte plus le plug-in Java, mais que Java est installé sur votre ordinateur, vous pouvez télécharger le fichier JNLP, enregistrez-le avant de l’ouvrir avec Java Web Start.

Dans l’applet précédente, vous pouvez aussi modifier la raideur des câbles (la modification sera prise en compte seulement si vous déplacez la charge). Vous pourrez aussi remarquer que dans certaines configurations, l’un des câbles n’est plus en tension (il est alors tracé en pointillé).

Et si l’on voulait aller au fond des choses, il faudrait prendre en compte encore un autre phénomène : les câbles ont leur propre masse qui fait que, même tendus, ils ne sont pas parfaitement droits (ils ont un profil en forme de chaînette). Pour être plus proche de la réalité, il faudrait prendre en compte cette déformation pour résoudre les modèles géométriques.

La multiplication des câbles, ou à trop diviser, on finit par ne plus régner

On pourrait penser intuitivement qu’en mettant un plus grand nombre de câbles (supérieur au nombre de degrés de liberté de la charge que l’on veut commander), on pourrait :

1. augmenter le volume de l’espace où l’on peut placer la charge,
2. mieux répartir les tensions dans les câbles (par exemple diminuer la tension dans un câble qui est proche de son point de rupture)

Les roboticiens utilisent le mot de redondance pour caractériser le fait que l’on dispose de plus de variables de contrôle que nécessaire. Notons toutefois qu’il y a un obstacle à la multiplication des câbles : le risque accru de collision entre eux.

L’augmentation du nombre de câbles va effectivement, en général, permettre de couvrir un espace de volume plus important. Par exemple, si l’on attache 4 câbles au même point d’une charge avec les treuils tous dans un même plan horizontal, les positions atteignables sont

• celles dont la projection dans le plan des treuils est incluse dans l’enveloppe convexe des points de départ des treuils (c’est-à-dire le polygone dont les arêtes sont des points de départ et qui contient l’ensemble des points de départ),
• celles qui ont une altitude maximum, qui dépend de la tension de rupture des câbles

Ainsi, ajouter un treuil permet effectivement d’agrandir l’espace atteignable, si le point de départ du nouveau treuil est en dehors de l’enveloppe convexe des autres points.

Par contre, la possibilité d’utiliser la redondance pour mieux répartir la tension entre les câbles fait encore débat. En contre-exemple, on a montré récemment que pour un robot à \(N>3\) câbles, tous attachés au même point sur la charge, on n’aura jamais plus de 3 câbles tendus simultanément (et même, dans certains cas, seulement un ou deux). La redondance introduite par les câbles supplémentaires ne permet donc pas de moduler les tensions dans les câbles. La généralisation de ce résultat est encore un problème ouvert.

Si le principe des robots parallèles à câbles est séduisant par sa simplicité apparente et par la richesse des applications potentielles, on a pu se rendre compte que de redoutables problèmes mathématiques se cachaient derrière cette simplicité. Ils peuvent être détournés en utilisant des géométries particulières (qui sont utilisées dans la très grande majorité des robots qui fonctionnent actuellement) ou tout simplement ignorés au détriment de la sécurité, pourtant essentielle pour des applications comme l’aide à la personne.

Les applets Java ont été écrites par Hadi Jaber, étudiant à l’ENSTA Bretagne, puis revues et complétées par Régis Monte.