Spams et hams… et comment les filtrer
Évidemment, pour l'individu lambda, ce n'est qu'une petite gêne de tous les jours, mais dès lors que l'on passe à l'échelle d'une entreprise, cela devient plutôt ennuyeux.
Imaginez le matin, en ouvrant votre boîte aux lettres, devoir commencer par trier les spams de tous les hams... Disons que vous perdez une à deux minutes, pas grand chose finalement. Mais si votre entreprise a dans les 5 000 employés, cela devient 5 000 fois 2 minutes, soit 10 000 minutes. Si on se rappelle que dans une journée de travail de 8 heures, il n'y a que 480 minutes, alors on découvre que ces spams coûtent à votre employeur 10 000 / 480 = plus de 20 jours, soit presque l'équivalent d'un mois de travail, et ceci tous les jours... Cela veut dire que votre patron pourrait employer des gens juste pour nettoyer les boîtes aux lettres électroniques.
- Vous voulez dire que tous les jours, une entreprise de 5 000 employés doit payer...
- Oui oui absolument !
- Première réaction : cela crée de l'emploi !
- Deuxième réaction : en fin de compte, c'est le client qui aura à payer ce surcoût... sans aucune amélioration de la qualité du produit fini.
De plus, on ne doit pas simplement considérer les spams comme des courriers anodins car souvent, ils ont un tout autre but que de vous faire perdre du temps.
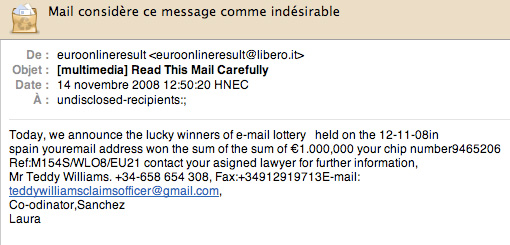
En général, ils vous demandent d'ouvrir un fichier compressé (qui contiendra un virus) ou alors de vous connecter à un site web pour vérifier vos coordonnées bancaires. Certains semblent venir de votre banque ou d'organismes connus comme Ebay ou Paypal. Dans ce cas, ils vous suggèrent généralement de vous connecter à un site pour vérifier vos coordonnées bancaires ou préciser des détails prétendument manquants.
Évidemment, les sites web cibles peuvent ressembler à s'y méprendre à d'autres sites tout à fait officiels, mais ce ne sont que des copies qui vont, si vous êtes coopérant, collecter des informations privées parfois cruciales comme votre numéro de carte bancaire... et alors là tout peut arriver. En anglais, on appelle « phishing » cette sorte de « pêche » à de l'information privée.
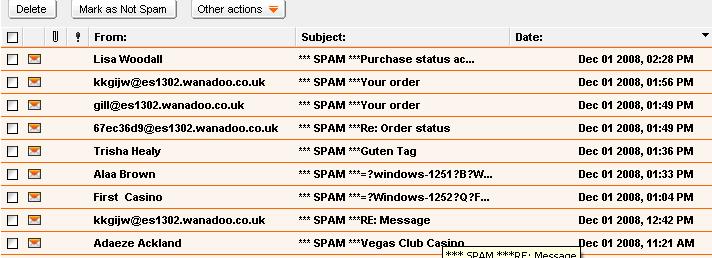
Exemple de boîte poubelle où l'on met les spams.
Le serveur les a identifiés comme spams et a modifié le sujet des messages pour l'indiquer au client. S'il n'y a pas ici le mot « loterie », il y a... « casino ». On remarque aussi que les adresses des émetteurs sont généralement fantaisistes, mais cela n'est pas si facile à détecter avec un programme.
Les spams sont donc non seulement gênants mais peuvent être porteurs de virus ou pire, récupérer à votre insu (mais avec votre coopération) des informations privées. La conclusion est alors simple : il faut absolument éliminer les spams de votre boîte aux lettres, et ceci de manière automatique si possible. Non seulement ce sera vraiment plus confortable pour tout le monde, mais cela évitera virus, fraudes et surcoûts...
C'est pour cela que l'on trouve aujourd'hui sur le marché un bon nombre de filtres à spam, appelés aussi filtres anti-spam, c'est-à-dire des programmes dont le seul objectif est de séparer les spams des hams. Ces programmes, qui tournent en permanence sur votre serveur de courrier électronique, ont la tâche délicate de vous indiquer que tel message est un spam, que tel autre ne l'est pas. Évidemment, ils se trompent de temps en temps, car ce n'est pas si simple ! Regardons pourquoi tout ceci est plus difficile qu'il n'y paraît à première vue, alors que vous... du premier coup d'œil... vous savez !
Le filtre à spam : que fait-il et où est-il ?
En gros, le filtre doit mettre dans votre boîte aux lettres les hams et dans votre poubelle les spams (on parle aussi de junk mail). En fait, cette méthode est un peu brutale : il peut se contenter de vous signaler la chose et ensuite c'est vous qui décidez.
Rappelons-nous que le courrier électronique fonctionne avec au moins deux acteurs :
- le client, c'est-à-dire vous qui lisez votre courrier électronique : on parlera de client mail pour désigner l'outil que vous utilisez pour lire votre courrier (Outlook, Thunderbird, et il y en a bien d'autres) ;
- le serveur, qui se charge d'envoyer votre courrier sortant et de mettre dans votre boîte aux lettres votre courrier entrant (sendmail, postfix, etc.).
L'idée est alors de se partager la tâche : le serveur déblaye grossièrement le terrain en testant les messages et en indiquant par un petit marqueur qu'il pense que le message en question est un spam. Lorsque vous consultez votre courrier en utilisant votre client mail, vous pouvez décider de faire confiance au serveur et de mettre directement à la poubelle les messages marqués spam... mais c'est assez dangereux en y réfléchissant bien.
Prenons un exemple simple : si un message comporte 10 fois le mot « loterie », il y a de fortes chances que cela soit un spam et votre serveur peut légitimement le considérer comme tel... mais si vous êtes le directeur de la loterie nationale, pour vous c'est un ham tout simplement. Il vaut donc mieux laisser au client le soin de prendre la décision finale. Le serveur nous donnera une indication utile, mais pas toujours pertinente.
En ce qui concerne les clients mail récents, on peut les configurer pour qu'ils jettent à la poubelle par exemple tous les messages dont le sujet contient le mot « loterie » (en supposant encore une fois bien sûr qu'on ne soit pas employé de la loterie nationale). En combinant ce type de règles, on peut finalement arriver à avoir une boîte aux lettres à peu près propre.... et même si on est très méticuleux, cette boîte aux lettres ne recevra plus de spams du tout, car ils seront tous automatiquement mis à la poubelle.
Cela paraît miraculeux, et pourtant, on ne peut pas se satisfaire de cette situation. En effet, de temps en temps, le système doit bien se tromper et jeter à la poubelle des messages importants ! Alors, à partir de quel moment sera-t-on réellement satisfait ?
Comme toujours lorsque l'on utilise des outils informatiques de prédiction (dans notre cas, servant à prédire les spams en vue de les éliminer), on s'intéresse à la performance de ces outils. Un point de vue assez évident est de considérer que cette performance se mesure par un pourcentage de succès. En d'autres termes, sur 100 messages, quel est le nombre de messages correctement identifiés comme spam ou ham ? Évidemment, ce pourcentage est très important... mais notoirement insuffisant pour nous satisfaire. Prenons à nouveau un exemple simple : supposons que l'on ait un taux de succès de 90 %... mais que tous les messages incorrectement identifiés soient des hams... En d'autres termes, notre filtre les considère comme des spams (on les appelle des faux positifs) et va donc les jeter dans notre poubelle. Ce qui signifie simplement que le matin, lorsque j'ouvre ma messagerie, je suis certain (ou presque) de ne pas avoir de spams dans ma boîte, mais je dois absolument aller vérifier ma poubelle pour être sûr que rien d'important n'a été jeté ! Dans ce cas, le filtre ne m'a pas simplifié la vie ; bien au contraire, puisque je dois faire moi-même le travail de tri dans la poubelle où tout est estampillé spam. En fait, je préfère avoir quelques spams résiduels dans ma boîte aux lettres (les faux négatifs), aisément identifiables, et être à peu près sûr de ce qu'il y a dans ma poubelle (pratiquement aucun faux positif) pour ne pas avoir à la visiter régulièrement.
On voit donc que pour mesurer la qualité d'un filtre à spam, on ne doit pas seulement s'intéresser à la précision absolue (qui est simplement la somme du pourcentage de faux négatifs et du pourcentage de faux positifs) mais différencier ces deux pourcentages pour avoir une idée plus précise du confort que nous apporte le filtre. Idéalement, il faut les maintenir bas tous les deux, mais on peut accepter un pourcentage de faux négatifs supérieur à celui des faux positifs. Nous reviendrons là-dessus par la suite.
Spam pour vous, ham pour moi !
Oui, vous l'avez compris... Si un message comporte 10 fois le mot « loterie », il y a de fortes chances que cela soit un spam, mais pour le directeur de la loterie nationale, c'est son pain quotidien. C'est-à-dire un message tout à fait normal, et peut-être important. De même pour beaucoup d'autres mots que l'on pourrait a priori considérer comme symptomatiques d'un spam, mais qui en fait n'en sont pas complètement caractéristiques. On a compris que le problème de la détection (et donc de l'élimination) des spams ne se résume pas à l'observation du contenu du message, mais demande l'analyse d'autres informations.
C'est aussi pourquoi, comme on l'a dit plus haut, on devra coupler un filtre général sur le serveur avec un filtre propre à l'utilisateur sur la machine cliente (à travers le client mail Outlook, Eudora ou Thunderbird).
La tâche est donc beaucoup plus complexe que prévu, et c'est pourquoi les techniques mises en œuvre doivent aussi être très astucieuses ! Regardons cela de plus près.
Les techniques de détection de spam
En fin de compte, un courrier est simplement un texte particulier passant par internet. Le filtrage spam/ham relève donc des techniques de classification en langage naturel. Les seules différences, et elles sont de taille, sont que non seulement la classification spam/ham dépend de l'utilisateur, mais que de plus il y a des adversaires (les spammers) qui cherchent en permanence à contourner nos outils ! D'où la difficulté.
Évidemment, il y a de nombreuses méthodes pour détecter un spam et il faut probablement les mixer pour arriver à quelque chose d'efficace. Essayons d'organiser nos idées.
Les techniques à base de règles
- Analyse de texte :
Il semble très naturel, pour distinguer un spam d'un ham, de rechercher dans le texte du courrier des mots qui seront considérés comme symptomatiques d'un spam. Si on trouve un certain nombre de ces mots, alors il y a de fortes chances que le message soit un spam. On comprend que, pour l'instant, la distinction entre spam et ham relève de l'analyse de texte. Pourquoi pas ? Mais alors se pose la question de savoir à partir de quel nombre d'occurrences du mot « loterie » ou de ses dérivés (pluriel, etc.) on considère que le message en question est un spam. Une autre idée simple est aussi d'identifier la langue dans laquelle est écrit le message. Vous pouvez décider que tous les messages qui vous arrivent en taïwanais sont des spams, car vous ne comprenez pas le taïwanais. - Analyse de l'en-tête - listes noires, blanches ou grises :
Une deuxième idée est de considérer, non plus le corps du texte, mais l'en-tête du message qui m'indique d'où il vient, par où il est passé, etc. Cela devient plus technique, mais on doit pouvoir en tirer des informations pertinentes. En effet, si je sais que tel site est un générateur de spams, alors si un courrier provient de cette adresse, il y a de grandes chances que ce soit un spam. D'où l'idée de tenir à jour une liste noire de sites considérés comme non fiables (émetteurs de spam), une liste de site sûrs (liste blanche) et enfin une liste de sites pour lesquels on hésite (liste grise). En analysant l'en-tête du message qui arrive, on voit tout de suite s'il entre dans l'une des trois catégories. Ce n'est que dans le cas de la liste grise qu'on va sérieusement analyser le contenu du message avant de décider. Ce type de filtres est largement implémenté dans les clients mail où l'utilisateur définit ses propres règles.
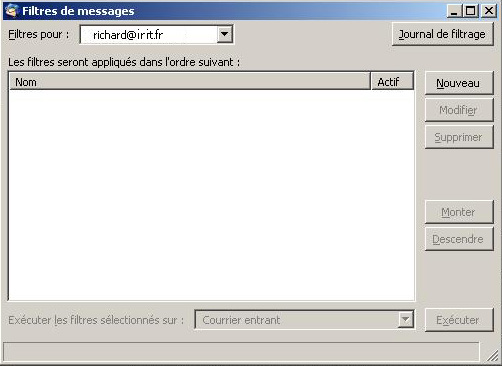
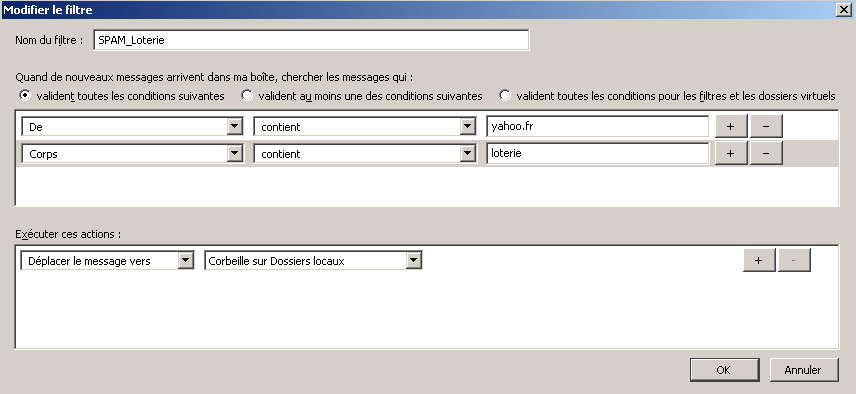
Les différents tableaux de bord de Thunderbird servant à définir nos règles de filtrage et à décider ce qu'on fera.
Du fait que certaines de ces règles vous sont propres, à l'intérieur de votre organisation, il est possible de mettre en œuvre des règles valides pour tout le monde sur le serveur de mail, et des règles spécifiques à chaque individu sur le client mail. En combinant ces différentes règles, on finit par avoir un système complet qui classifie un message comme spam ou ham selon qu'il satisfait les règles ou non, et qui le met dans votre boîte normale ou dans votre poubelle.
Les techniques probabilistes
L'idée qui est mise en œuvre ici est d'un esprit différent des précédentes. Avec les techniques à base de règles, si le message que l'on examine satisfait certaines conditions, alors c'est un spam : on dispose en effet de règles qui décident de la classification du message. Maintenant, on va plutôt calculer par des méthodes probabilistes la probabilité qu'un message soit un spam, sachant qu'il vérifie un certain nombre de propriétés. Si cette probabilité est grande, qu'elle dépasse un certain seuil, alors on considèrera le message comme spam, dans le cas contraire il sera vu comme ham. Pour ce faire, on va, à partir de messages que l'on a déjà classifiés (on parle de base d'apprentissage), construire un réseau appelé réseau bayésien, qui nous permettra de calculer la probabilité du nouveau message d'être un spam.
Introduite dans les années 1990, cette technique s’est avérée extrêmement puissante et tout à fait satisfaisante pour de nombreuses tâches d’apprentissage. L’idée essentielle est de calculer la probabilité d’un événement donné en fonction de la probabilité d’autres événements préalablement observés. Pour notre thème des spams, on se pose la question, étant donné un nouveau message, de savoir si c’est un spam, sachant par exemple qu’il contient 3 fois le mot « loterie », qu’il arrive de yahoo.fr, qu’il ne comporte aucun code HTML et aucune image.
Intuitivement, on comprend que cette probabilité dépend de la probabilité d’être un spam sachant qu’on vient de yahoo.fr, de la probabilité de venir de yahoo.fr sachant qu’on contient 3 fois le mot « loterie », pas de code HTML et pas d’image, de la probabilité…
Bien, mais la probabilité d’être un spam sachant que l’on vient de yahoo.fr, comment la connaître ? Eh bien, on peut par exemple constater, sur le serveur, que sur 100 000 messages venant de yahoo.fr, environ 35 000 sont des spams. Parfait, on va dire que la probabilité que l’on cherche est de 35 000/100 000, soit à peu près 1/3. Et on continue de cette manière. À partir de toutes ces probabilités connues et préalablement stockées dans des tables, on va très vite calculer la probabilité cherchée. Si cette probabilité dépasse un certain seuil que l’on va fixer, alors on décidera que le message en question est un spam.
Évidemment, il y a des erreurs, mais on s’aperçoit que les techniques utilisant les réseaux bayésiens donnent généralement de bons résultats. La littérature est très abondante sur le sujet et on se reportera avec profit au livre Les réseaux bayésiens, P. Naïm, P. Wuillemin, P. Leray, O. Pourret, A. Becker, Eyrolles 2004.
Lire aussi sur Interstices : Les réseaux bayésiens.
Prenons un exemple pour comprendre. Supposons que nous recevions un message en provenance du domaine yahoo.fr et qui contient 5 fois le mot « loterie ». La question qui se pose est « spam ou ham ? ». D’un point de vue probabiliste, il s’agit de calculer la probabilité d’être un spam sachant que l’on provient de yahoo.fr et que l’on contient 5 fois le mot « loterie ». En mathématiques, on parle de probabilité conditionnelle, et cette probabilité est simplement égale au rapport de deux autres probabilités :
- la probabilité de tout cumuler en même temps : être un spam et provenir de yahoo.fr et contenir 5 occurrences du mot « loterie » ;
- la probabilité de simplement venir de yahoo.fr et de contenir 5 occurrences de « loterie ».
Le réseau bayésien permet justement de calculer ces deux nombres en combinant des informations élémentaires préalablement stockées (par exemple le fait que 5 % des messages reçus de yahoo.fr sont des spams, que 10 % des spams contiennent le mot « loterie », etc.). Si le résultat final donne 0,3, alors on peut considérer que le message est un ham, si on trouve 0,8, on peut considérer que c’est un spam. On comprend donc que le filtre va devoir, entre autres, se fixer un seuil de probabilité au delà duquel il décide « spam ». Évidemment, si le seuil est trop haut, alors on laisse passer un grand nombre de spams qui vont polluer la boîte aux lettres… ce qui n’est pas l’objectif poursuivi. L’ajustement des seuils est toujours un exercice délicat !
On peut multiplier le nombre de paramètres à prendre en compte et donc complexifier le calcul mais il reste dans la même logique de combinaison, et l’ordinateur l’exécute aisément pour classifier le message.
Il se trouve que ces techniques sont très performantes et la plupart des filtres les implémentent en les combinant avec des règles et en ajustant des paramètres pour optimiser les résultats.
Les techniques à base de compression
Implémentées plus récemment (voir par exemple l’excellent article Spam filtering using statistical data compression models de A. Bratko, G. V. Cormack, B. Filipic, T. R. Lynam, et B. Zupan, paru en 2006 dans le Journal of Machine Learning), ces techniques sont probablement pour l’instant encore du domaine de la recherche et de l’expérimentation. Elles visent à éliminer la partie analyse textuelle propre aux filtres anti-spam, et même à ne pas tenir compte de la structure du message séparant l’en-tête avec source/destination/sujet et le corps du courrier.
Intuitivement, l’idée est simple : les spams doivent d’une certaine manière avoir des contenus en information similaires entre eux, de même pour les hams. Si on est capable de mesurer (par un nombre) ce contenu en information, alors on doit pouvoir s’en servir. On peut se baser sur des théories de l’information pour avoir des soubassements théoriques séduisants.
En fait, généralement, quand on fait référence à la théorie de l’information, on pense à celle de Claude Shannon. Dans notre document, nous nous référons plutôt à ce que l’on appelle parfois la théorie de la complexité algorithmique de Kolmogorov (voir aussi le document Théories et théorie de l’information).
Mieux connu pour ses travaux sur la théorie des probabilités, Kolmogorov s’est aussi intéressé à la notion d’information et en a donné une définition absolue en quelque sorte : la complexité de Kolmogorov K(s) d’une chaîne de caractères s n’est autre que la taille du plus petit programme pouvant produire cette chaîne sur une machine de Turing universelle. Comme tout ce que l’on manipule sur un ordinateur est en fin de compte une chaîne de 0 et 1, cette définition est valide aussi pour nos spams et hams. Évidemment, on doit ajouter pas mal de détails techniques pour aboutir à quelque chose qui fonctionne, mais l’essentiel est dit.
Dans ces conditions, K(s), qui est donc un nombre entier, peut être vu comme la quantité d’information contenue dans la chaîne s puisque, si on raccourcit ce petit programme, alors il n’y a plus moyen de générer s. On peut aussi voir les choses en disant que K(s) est la compression ultime de s… d’où l’idée d’estimer ce nombre idéal K(s) simplement en compressant s. Meilleure sera la compression C(s), et plus la taille du fichier C(s) sera proche du nombre K(s).
À partir de là, on comprend que si on concatène 2 fichiers a et b (on note le résultat a.b), et que K(a.b) est proche de disons K(a), cela signifie que b n’apporte pas grand chose de nouveau : l’information contenue dans b l’était déjà dans a ! Il suffit alors de combiner K(a), K(b), K(a.b) pour obtenir un nombre d(a,b) qui satisfait toutes les propriétés d’une distance. On appelle cette distance la distance informationnelle. Et on peut alors utiliser les outils classiques de data mining qui nécessitent une distance (entre autres l’algorithme des k-plus proches voisins).
Ensuite, comme souvent en informatique, se pose la question du calcul ou de l’estimation de ce contenu en information. Et là, il apparaît que ce contenu en information peut s’approcher en compressant le texte et en calculant la taille du fichier compressé. Dit abruptement, le contenu en information I(m) du message m c’est la taille du fichier m.zip… pas plus que cela…. Et cela nous ouvre pas mal d’horizons.
Tout le monde a été confronté au problème de l’envoi de fichiers attachés dans des courriers électroniques qui sont trop volumineux et sont refusés par le serveur. Une solution est de compresser le fichier, afin d’obtenir un fichier plus petit que l’on envoie et que le destinataire décompressera avec l’outil approprié. Et donc, tout le monde a déjà utilisé des utilitaires de compression comme winzip avec Windows ou compress avec Unix. Avec le développement de l’internet, les outils de compression sont devenus indispensables.
Les techniques de compression sont très sophistiquées, mais on peut intuitivement comprendre que, si un schéma se répète très fréquemment dans le fichier que je souhaite envoyer, alors je dois remplacer ce schéma par un code court, alors que pour un schéma qui est peu fréquent, on peut accepter un code plus long.
Par exemple, si je veux compresser ABCABCDABCDABC, je vois que ABC apparaît 4 fois, AB aussi, CD 2 fois, ABCD 2 fois également, etc. On peut alors dire que l’on remplace ABC par A, et on laisse D inchangé, ce qui donne AADADA. En raffinant ce type de raisonnement, on voit que l’on peut sérieusement réduire la taille d’un fichier à envoyer, pour peu que l’on envoie également l’information que A représente ABC. Et la taille de cette table est en fait ridicule dès lors que le fichier à transmettre est gros : dans ce cas, la compression sera vraiment effective. On comprend que pour bien compresser, on a besoin de régularité dans le fichier, sinon on compressera peu.
D’autre part, si on sait que le destinataire ne voit pas la lettre D, il n’y a qu’à la supprimer du fichier compressé et envoyer AAAA. Le destinataire, quand il décompressera, ne verra que ABCABCABCABC, mais il ne se rendra pas compte de la différence. Par opposition aux algorithmes sans perte, on parle de compression avec perte – un bon exemple en est le format de compression MP3 qui supprime des fichiers musicaux les fréquences inaudibles pour l’oreille humaine.
Évidemment, pour produire une approximation de la complexité de Kolmogorov, on s’intéresse à des algorithmes sans perte, qui sont utilisés dans des utilitaires comme winzip, winrar, compress, etc.
Ensuite, le raisonnement est peu ou prou le suivant. On dispose d’une base de messages déjà classifiés spam/ham. À l’arrivée d’un nouveau message, on calcule son contenu en information. À ce stade, plusieurs démarches sont possibles :
- Soit on calcule le contenu en information de la base de hams et de la base de spams. Puis on ajoute à la base de hams (respectivement spams) le courrier entrant. Et on calcule le différentiel pour répondre à la question : est-ce que ce message ajoute plus d’information à la base de hams ou a la base de spams ? Ce différentiel est appelé parfois « la surprise ». Si la surprise est faible avec les spams, cela signifie que le courrier en question apporte peu d’information à la base des spams, donc que son contenu informatif est déjà plus ou moins contenu dans cette base, donc il s’agit d’un spam. Même raisonnement pour les hams !
- Une autre technique est d’utiliser l’algorithme des k-plus proches voisins. En effet, en notant I(m) le contenu en information d’un message m, la théorie de l’information nous dit que si pour deux messages m et n, on calcule 1 – (I(m) + I(n) – I(mn))/max(I(m), I(n)) alors on obtient une distance au sens mathématique du terme. Comme on a vu que finalement I(m) est simplement estimé par la taille de m.zip, il n’y a pas de difficulté à calculer la distance d’un message entrant avec tous les messages de la base. On choisit par exemple les 11 messages de la base les plus proches du message entrant et si parmi ces 11 messages, on a une majorité de spams, on décide que le message entrant est un spam… sinon un ham… Ce n’est pas plus compliqué que ça !
L’algorithme des k-plus proches voisins est un des algorithmes de classification les plus simples. Le seul outil dont on a besoin est une distance entre les éléments que l’on veut classifier. Si on représente ces éléments par des vecteurs de coordonnées, il y a en général pas mal de choix possibles pour ces distances, partant de la simple distance usuelle (euclidienne) en allant jusqu’à des mesures plus sophistiquées pour tenir compte si nécessaire de paramètres non numériques comme la couleur, la nationalité, etc.
Comment cela marche-t-il ? On considère que l’on dispose d’une base d’éléments dont on connaît la classe. On parle de base d’apprentissage, bien que cela soit de l’apprentissage simplifié. Dès que l’on reçoit un nouvel élément que l’on souhaite classifier, on calcule sa distance à tous les éléments de la base. Si cette base comporte 100 éléments, alors on calcule 100 distances et on obtient donc 100 nombres réels. Si k = 25 par exemple, on cherche alors les 25 plus petits nombres parmi ces 100 nombres. Ces 25 nombres correspondent donc aux 25 éléments de la base qui sont les plus proches de l’élément que l’on souhaite classifier. On décide d’attribuer à l’élément à classifier la classe majoritaire parmi ces 25 éléments. Aussi simple que cela. Bien sûr, on peut faire varier k selon ce que l’on veut faire, on peut aussi complexifier la méthode en considérant que les votes des voisins ne sont pas de même poids, etc. Mais l’idée reste la même.
Il se définit facilement en mathématiques comme une fonction d d’un espace de données X × X dans l’ensemble des réels R telle que :
- d(x,y) > 0 sauf si x = y
- d(x,y) = d(y,x) (symétrie)
- et enfin l’inégalité triangulaire d(x,y) < d(x,z) +d (z,y).
En fait, le concept est très utile en data mining puisqu’on part du principe suivant : « qui se ressemble s’assemble »… et on l’applique à l’envers : « qui s’assemble se ressemble ». Ainsi, dès lors que l’on dispose d’une distance sur un espace de données, on pourra dire que si la distance entre 2 données est faible, elles partagent les mêmes caractéristiques. En ce qui nous concerne, si un message est « près » d’un autre qui est un spam, alors lui-même peut être considéré comme un spam. Le raisonnement est plutôt abrupt, mais convenablement appliqué et pondéré, il donne de bons résultats.
- Un peu plus sophistiqué maintenant : au lieu de considérer un algorithme de classification aussi simple que les k-plus proches voisins, on va utiliser des outils plus élaborés. En fait, à partir du moment où on dispose d’une distance, de nombreuses techniques de classification deviennent disponibles. Si on a comme précédemment une base d’exemples pour lesquels on connaît la classe (spam ou ham), on peut choisir un ensemble de, disons, 5 messages estampillés spam et 5 messages ham. Il est possible de calculer la distance informationnelle du message entrant avec ces différents messages : on obtient un ensemble de 10 nombres réels qui caractérisent un message et le représentent comme un vecteur à 10 composantes. Supposons que l’on dispose d’une base de messages dont on connaît la classe, chacun de ces messages étant représenté par un vecteur à 10 composantes. On peut donc entraîner sur cette base une SVM (Support Vector Machine) qui va nous fournir un classificateur que l’on pourra utiliser pour classifier les messages entrants. Ce type de technique fournit des résultats assez surprenants : une précision de l’ordre de 97 % avec un taux de faux positifs inférieur à 1,2 %… et ceci sans aucune analyse textuelle. En théorie, il ne reste plus qu’à les mixer avec les techniques classiques pour, peut-être, obtenir les meilleurs filtres !
Il s’agit d’une technique de classification très sophistiquée, avec des fondements théoriques très solides, développée par Vladimir Vapnik et ses collègues en 1992 et qui continue à avoir beaucoup de succès. L’idée, simple au départ, est de chercher à séparer par une droite (un hyperplan) des points sur un plan. Supposons que l’on ait un ensemble de points noirs et un ensemble de points blancs, on cherche à faire passer une droite telle que tous les blancs soient d’un côté et les noirs de l’autre… Pas simple, parfois impossible… il faut tordre un peu la droite ! Mais si on y arrive, il est évident qu’il n’y a pas qu’une seule droite qui fasse le travail. En décalant la droite très légèrement, on peut sûrement encore séparer les noirs des blancs.
Parfait, mais alors se pose la question de la meilleure droite, enfin disons celle qui a le plus de chance d’avoir de bons résultats quand de nouveaux points vont arriver. Une idée simple est de choisir la droite qui est la plus loin des points qu’elle sépare. Intuitivement, on pourrait dire que l’on prend une position la moins tranchée possible… on dit que l’on maximise la marge avec les exemples.
Bravo, mais comment calculer cette droite (si elle existe) ? Il y a des algorithmes qui font cela parfaitement. D’accord, mais quand on ne peut pas séparer les points par une droite ? Effectivement, dans ce cas, au lieu de considérer que ces points sont dans un simple plan, on va les « plonger » dans un espace de plus grande dimension… et si on a une dimension assez grande, on démontre que l’on peut trouver un tel hyperplan. Il ne reste plus qu’à projeter cet hyperplan sur notre plan habituel à 2 dimensions et on obtiendra… une courbe qui séparera nos points. On n’a plus une simple droite, mais ce n’est pas grave : on sépare nos points et donc on les classifie, c’est le principal. Et tout ceci s’applique parfaitement aux messages que l’on veut classifier spam/ham !
Les techniques mixtes et non dévoilées !
Bien entendu, si on a une bonne connaissance de la logique des filtres diffusés librement et open source, il n’en est pas de même des filtres commerciaux protégés par des brevets et dont le code est inconnu. Et il y en a de nombreux.
On se doute qu’ils utilisent plus ou moins une mixture des méthodes indiquées précédemment, mais en y ajoutant leur grain de sel. En fait, on a compris qu’il y a un nombre infini de possibilités pour construire un filtre, il suffit simplement d’adapter quelques-uns des innombrables paramètres dont nous avons parlé précédemment. Dès lors que l’on aboutit à un comportement satisfaisant sur des bases de test sérieuses, alors on peut considérer que l’on a un bon filtre et le mettre sur le marché !
Un petit bilan
Et dans la vie de tous les jours, ça donne quoi ? En fait, en se connectant sur Internet, il est facile de trouver des sites commerciaux diffusant des filtres anti-spam. Souvent, il est difficile de faire la part du discours marketing et des performances réelles. Il n’est pas rare de voir des sites annoncant 99 % de réussite (ce qui, comme on l’a vu, doit être décomposé en faux positifs et faux négatifs). Quoi qu’il en soit, 99 % de précision est un beau resultat. La réalité est en général un peu différente.
Il y a d’abord la perception que les gens ont de cette précision, car personne ne la calcule exactement. Des sondages montrent que les usagers, en moyenne, estiment à 85 % la performance de leur filtre. Cela signifie que si on vous demande combien vous recevez de spams dans votre boîte aux lettres pour 100 courriers reçus, vous allez probablement indiquer un chiffre autour de 15. Donc, finalement, votre perception de la précision est inférieure à 85 %, car vous ne parlez en général que des faux négatifs (spams non identifiés comme tels) et pas des faux positifs (les hams dans votre poubelle).
D’un point de vue plus rigoureux, il existe des bases de données de testsur lesquelles on peut tester les filtres. Par exemple, la base de données Enron qui contient tous les messages échangés dans la société durant sa dernière année d’existence. Spamassassin, un filtre anti-spam bien connu, dispose lui-même d’une base de données très conséquente sur laquelle on peut effectuer des tests.
Il existe un corpus assez volumineux de courriers électroniques qui peut servir de test pour vérifier la qualité d’un filtre. Par exemple, TREC ou même FERC (plus d’un million de messages) qui regroupent les courriers électroniques diffusés dans la société Enron (Enron corpus) ou alors le corpus de Spamassassin. Pour des explications détaillées sur la conception de ces bases de données, on peut se reporter aussi aux travaux de Bryan Klimt et Yiming Yang (voir le document PDF à télécharger) et ceux de Gordon Cormack et Thomas Lynam (voir le document PDF à télécharger). Ces corpus sont indispensables pour tester la qualité d’un filtre avant de le mettre sur le marché.
Du côté du client, il n’y a pas grand chose à faire pour activer et optimiser son filtre anti-spam. Par défaut, votre client mail utilise les informations venant du serveur, active vos règles si vous en proposez (en général, cette option vous est accessible via un outil de l’onglet de configuration), met en œuvre un filtre bayésien par défaut qui sera mis à jour automatiquement. En effet, quand un message arrive classifié comme spam, vous avez toujours l’option de décider que cela n’en est pas un, auquel cas le filtre va réviser son mécanisme pour prendre en compte le fait qu’il s’est trompé sur ce message. Comme probablement très peu de gens utilisent ce genre d’outil mis à disposition par leur client mail, il vaut mieux s’en remettre au serveur et espérer que celui-ci dispose d’un filtre efficace. La tâche revient donc à l’administrateur de votre serveur mail : choisir un bon filtre, l’installer et le mettre à jour.

L’un des filtres à spam les plus connus.
Un bon exemple, bien connu des administrateurs Linux, est Spamassassin. Il s’agit simplement d’un package que l’on installe sur le serveur et qui tourne en tâche de fond. Spamassassin récupère un message, le traite et ensuite l’envoie au serveur mail. Le traitement est une batterie de tests qui aboutit à la classification. Parmi ces tests, certains recherchent des mots clés : cette liste de mot clés est stockée dans un fichier mis automatiquement à jour sur internet (un peu comme un anti-virus). En ce qui concerne les listes noires, la même méthode de mise à jour est utilisée. À la fin de tout ces tests, le message reçoit un score, disons entre 0 et 5, 0 signifiant ham presque sûr, 5 signifiant spam presque sûr. L’administrateur peut alors ajuster un seuil pour décider de classer un message. Par exemple, si le seuil est 3, cela signifie que l’on considère comme ham tous les messages ayant un score inférieur ou égal à 3. Si on s’aperçoit qu’il y a trop de spams qui passent inaperçus, alors on peut décider d’abaisser la barre à 2 : cela devient plus difficile d’être considéré comme un ham donc il y aura moins de spams dans votre boîte aux lettres… mais attention aux faux positifs, qui seraient faussement estampillés spam. En d’autres termes, l’administrateur doit en permanence surveiller ces seuils. Quand un message reçoit un score qui le classifie comme spam, alors son en-tête est modifié pour indiquer au client qui viendra le lire que ce message est considéré comme un spam. Ensuite, à vous de décider ce que vous en faites !
En termes de prix, le paysage est varié. On peut bien sûr se limiter à des filtres entièrement gratuits, comme Spassassin qui est le plus connu. Quand on passe à des produits commerciaux, alors on s’intéresse essentiellement à des filtres qui seront installés côté serveur. Ces filtres s’adressent donc à des entreprises et non à des particuliers. Si les moins chers (pour une dizaine d’utilisateurs) ont un coût de l’ordre de la dizaine d’euros, ceux permettant de traiter plus de 2 000 utilisateurs peuvent dépasser les 30 000 euros… Cela prouve simplement que les entreprises sont prêtes à investir des sommes non négligeables pour arrêter les spams !
Conclusion
La détection des spams reste un problème dont la solution est complexe. Sans oublier le fait que ceux qui envoient des spams sont aussi des gens avisés qui ont une bonne connaissance des techniques de filtrage, largement diffusées. Avec l’ouverture d’internet, on est dans la situation suivante où le défenseur dit publiquement « je ne veux pas recevoir vos messages et je vais employer ces méthodes pour les éliminer »… Il est clair que celui qui envoie les spams possède alors tous les éléments nécessaires pour imaginer une technique de contournement. C’est pourquoi, aujourd’hui, on reçoit de plus en plus de spams qui ne comportent pas de texte… mais uniquement une image qui elle contient le texte. En d’autres termes, on reçoit un fichier .gif ou .jpg qui est en quelque sorte une photo du message texte que le spammer souhaite diffuser. Et alors ? Eh bien, le problème de la détection des spams n’est plus dans ce cas un problème d’analyse de texte mais un problème d’analyse d’image… infiniment plus complexe. Bravo ! Les spammers adaptent aussi leurs techniques pour contourner les filtres ! Ce qui signifie que :
- il y a encore du pain sur la planche ;
- cela risque de ne jamais finir !
Enfin, n’oublions pas que de plus en plus, on utilise Internet pour faire de la téléphonie, c’est-à-dire transmettre des données vocales (par exemple avec Skype). Dès lors, il devient facile d’envoyer des sortes de spams « vocaux » : on appelle cela des spits (SPam over Internet Telephony). Ce n’est que le début… Ne parlons pas de la télévision !
Comme vous le voyez, on est encore loin d’un internet spam free ! Rendez-vous l’année prochaine pour faire le point ?
Newsletter
Le responsable de ce traitement est Inria. En saisissant votre adresse mail, vous consentez à recevoir chaque mois une sélection d'articles et à ce que vos données soient collectées et stockées comme décrit dans notre politique de confidentialité
Niveau de lecture
Aidez-nous à évaluer le niveau de lecture de ce document.
Votre choix a été pris en compte. Merci d'avoir estimé le niveau de ce document !

Gilles Richard