
« La science, contrairement à ce que l’on dit parfois, ce ne sont pas des réponses triviales à des questions complexes ; c’est toujours une invitation à la subtilité. »
(Propos d’Aurélien Barrau, astrophysicien, lors de son intervention à TEDx Marseille en 2018)
Le monde qui nous entoure est dynamique, foisonnant, enchevêtré, entortillé, subtil, riche… bref, complexe. Je ne vais pas expliquer comment on a démontré que « tout est complexe », mais plutôt tâcher d’expliquer ce que signifient « tout » et « complexe » dans ce résultat à la frontière entre les mathématiques et l’informatique.
Des circuits pour tout encoder
Les graphes sont des objets mathématiques très polyvalents, capables de modéliser de nombreuses situations. Un graphe décrit une relation entre les éléments d’un ensemble (appelés sommet) : les flèches (appelées arêtes) indiquent quels éléments sont reliés à quels autres (la relation n’est pas forcée d’être symétrique : \(a\) peut être relié à \(b\), sans que \(b\) soit relié à \(a\)). Par exemple les sommets peuvent représenter les dispositions du jeu Chomp sur une tablette de taille \(3×3\), et les arêtes la stratégie suivie par l’un des deux joueurs (indiquant le prochain coup à jouer). Ou alors les sommets peuvent représenter un disque découpé en cinq quartiers dont chacun est blanc ou noir, et les arêtes l’évolution observée lorsque chaque quartier prend la couleur majoritaire parmi sa propre couleur et celle de ses deux voisins. Ou encore les sommets peuvent représenter les nombres entiers positifs, avec pour chaque nombre \(x\) une arête qui part de \(x\) vers le nombre \(y\) choisi selon la fameuse formule de la suite de Syracuse : si \(x\) est pair alors l’arête va vers \(y = \frac{x}{2}\), et si \(x\) est impair alors l’arête va vers \(y = 3x + 1\). Les variations sont infinies.
Dans les exemples de la figure 1 ci-dessous, il y a exactement une arête qui part de chaque sommet. Les processus modélisés sont discrets (par opposition à continus) et déterministes (par opposition à aléatoires) : chaque disposition possède un unique successeur. Il s’agit d’un point de vue courant pour expliquer certains mécanismes à la base des phénomènes naturels, où l’on recherche des lois permettant de prédire avec exactitude le futur.
Pour parler d’un graphe précis, on peut le décrire en français, le dessiner, ou simplement lister ses sommets et toutes ses arêtes. Il existe de nombreuses façons d’encoder un graphe donné, et il s’agit d’un véritable enjeu pour les graphes de très grande taille. On commence souvent par numéroter les sommets de 0 à \(n – 1\) avec \(n\) le nombre de sommets, que l’on écrira en binaire sur \(log\)2(\(n\)) bits, en bon(ne) informaticien(ne). Dans les graphes qui nous intéressent ici, de chaque sommet sort exactement une arête, donc nous pouvons encoder chaque graphe comme une simple liste de sommets, ordonnés de façon à ce que le \(i\)-ème sommet de la liste désigne le numéro du sommet d’arrivée de l’arête partant du sommet numéro \(i\). Chaque numéro de sommet apparaît dans la liste autant de fois que le sommet désigné a de prédécesseurs. Cette liste peut en outre être encodée de façon encore plus succincte, grâce aux circuits booléens.
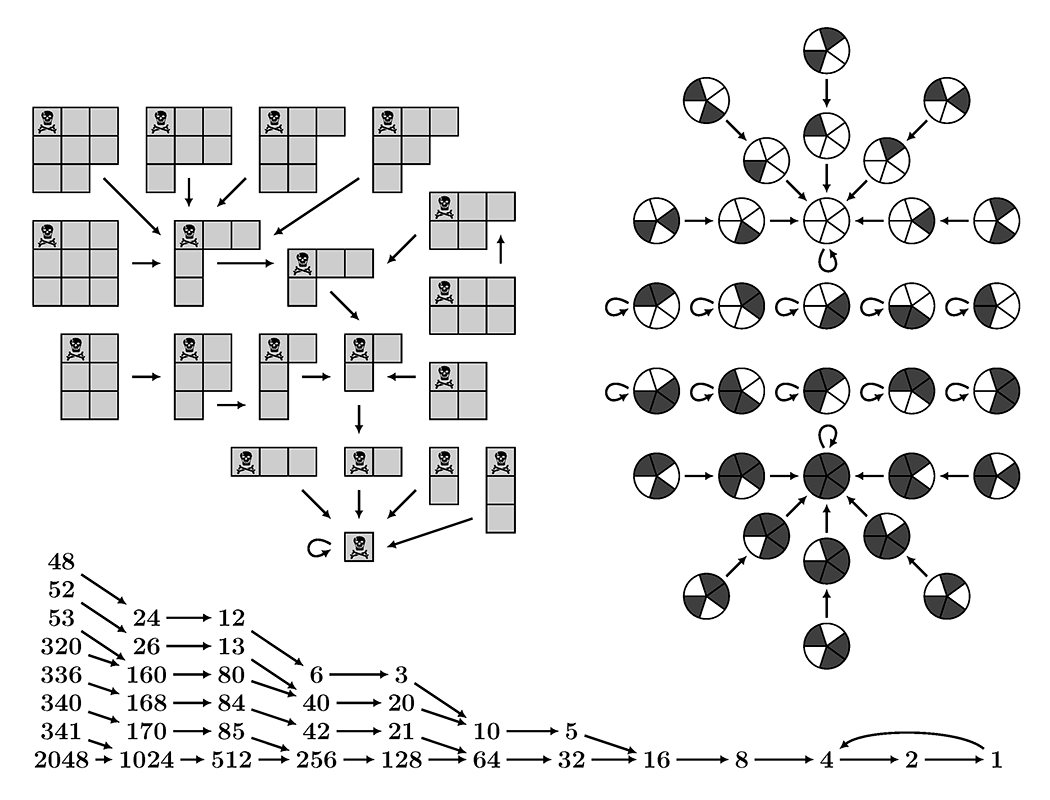
Figure 1 – Exemples de graphes : stratégie pour le jeu Chomp, évolution de cinq quartiers selon la règle de majorité, et suite de Syracuse pour les entiers à distance au plus onze de \(1\).
Un circuit booléen est un graphe (un graphe pour encoder un graphe !), possédant cinq types de sommets : des entrées, des portes et, ou, non, et des sorties. Des arêtes relient ces sommets en respectant les contraintes suivantes : aucune arête ne pointe sur les entrées, deux arêtes pointent sur chaque porte et et chaque porte ou, et une arête pointe sur chaque porte non et chaque sortie. Lorsqu’on place un bit (\(0\) ou \(1\)) sur chaque sommet d’entrée, le circuit booléen opère un calcul qui place un bit sur chaque porte : selon les bits pointant vers les portes et, ou et non, celles-ci réalisent l’opération booléenne correspondante, jusqu’aux sommets de sorties qui recopient le bit du sommet qui pointe sur eux. Pour que le calcul s’opère correctement, un circuit booléen ne doit pas posséder de cycle : le calcul associe, pour chaque nombre binaire placé sur les entrées, un nombre binaire placé sur les sorties. Ainsi avec \(log\)2(\(n\)) entrées et \(log\)2(\(n\)) sorties, on encode un graphe à \(n\) sommets : pour connaître le sommet pointé par l’arête partant du sommet numéro \(i\), il suffit de placer le nombre binaire \(i\) sur les entrées du circuit, et de lire la réponse sur les sorties du circuit (voir la figure 2 ci-dessous). Par exemple, sur le premier circuit, pour l’entrée \(8\) qui s’écrit \(1000\) en binaire, nous plaçons \(1,0,0,0\) sur les 4 sommets en entrées, exécutons le circuit booléen et obtenons comme résultat \(1,1,1,0\), qui code en binaire le nombre \(14\). Ainsi le sommet \(8\) de ce graphe a pour successeur le sommet \(14\). Le second circuit de la figure 2 possède \(10\) sommets, et il encode un graphe à \(16\) sommets dont toutes les arêtes pointent vers le sommet numéro \(0\) (car \(b ∧ ¬ b = 0\) quelle que soit la valeur du bit \(b\)). En généralisant cet exemple, on obtient un circuit à \(2n + 2\) sommets pour encoder un graphe à \(2\)\(n\) sommets, soit une économie exponentielle ! On parle de représentation succincte de graphe.
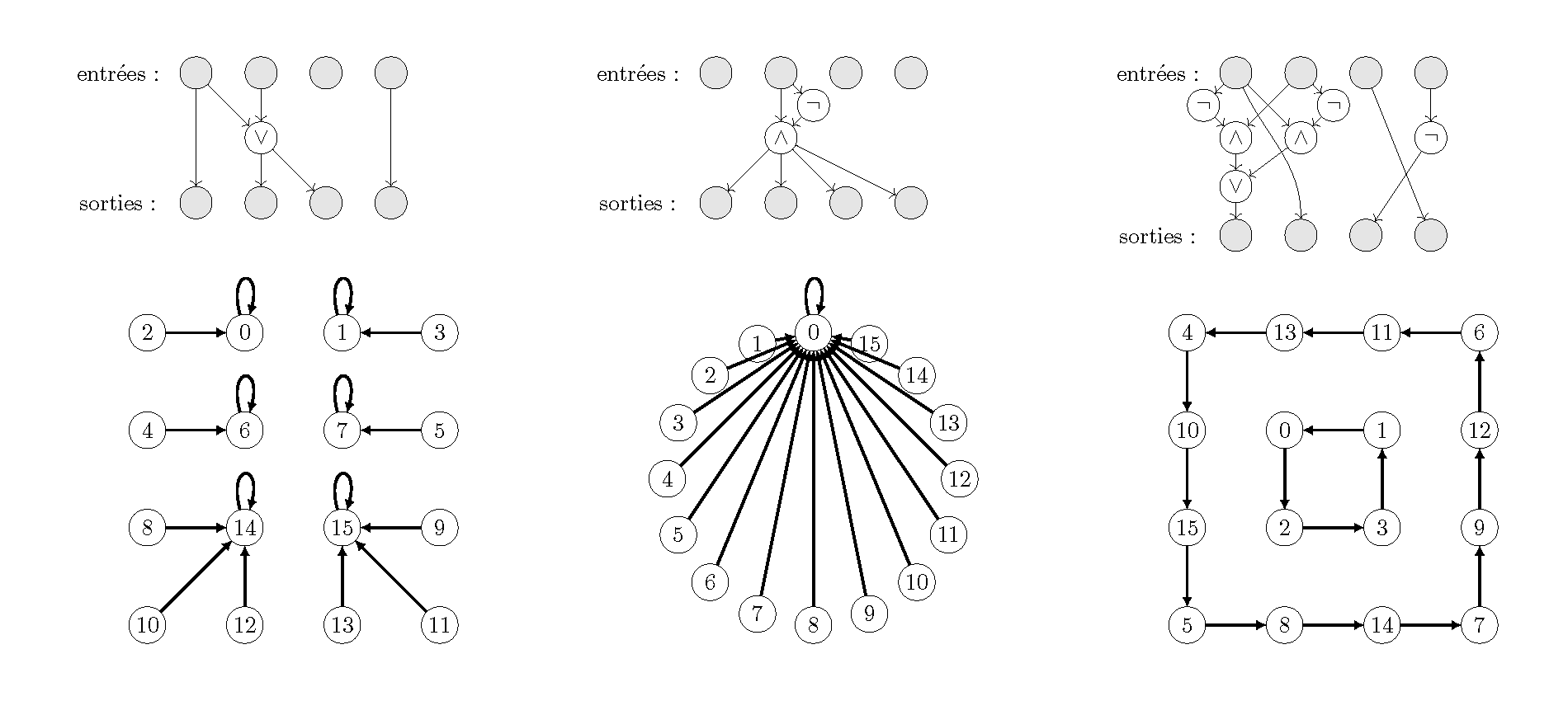
Figure 2 – Exemples de circuits (en haut) et les graphes encodés (en bas) : pour \(n = 16\) sommets on code les numéros des sommets en binaire sur \(4\) bits (de \(0000\) à \(1111\), avec le bit de poids faible à droite). On note respectivement \(∧\), \(∨\), \(¬\) pour désigner les portes et, ou, non.
Des formules pour poser des questions
Pour comprendre le monde qui nous entoure, on pose des questions auxquelles on souhaite obtenir des réponses. Ces questions peuvent se ramener à une ou plusieurs questions décisionnelles, c’est-à-dire dont la réponse est « oui » ou « non ».
Par exemple, si l’on pose une question dont la réponse est un nombre, alors cette question peut être décomposée en plusieurs questions décisionnelles afin de calculer bit-à-bit la solution : le premier bit est-il \(1\) ? le second bit est-il \(1\) ? le troisième bit est-il \(1\) ? etc.
Nous poserons des questions sur les graphes en utilisant un langage simple et d’une grande clarté : la logique du premier ordre. Dans cette logique, on peut construire des phrases mathématiques (appelées formules) en assemblant les morceaux suivants (où \(u\),\(v\),\(w\) désignent des sommets) :
| Symbole mathématique | Signification |
| \(∃u\) | il existe un sommet \(u\) tel que |
| \(∀u\) | pour tout sommet \(u\) |
| \(u=v\) | \(u\) et \(v\) désignent le même sommet |
| \(u→v\) | l’arête sortant de \(u\) pointe vers \(v\) |
| \(∧\) | et |
| \(∨\) | ou |
| \(¬\) | non |
Par exemple la formule \(∃u\) \(∀v\) \(v\) \(→\) \(u\) signifie « il existe un sommet \(u\) tel que pour tout sommet \(v\) l’arête sortant de \(v\) pointe vers \(u\) », c’est-à-dire que les arêtes pointent toutes vers le sommet \(u\). On ajoute des parenthèses pour éviter les ambiguïtés, comme pour la formule \(∀u\) \(∃v\) \((v → u)\) \(∧\) (\(∀w\) \((w = v)\) \(∨\) \(¬\)\((w → u))\) qui indique que chaque sommet \(u\) est pointé par exactement un sommet \(v\), car tout autre sommet \(w\) pointe ailleurs. Étant donné un graphe, qui est un objet fini à \(n\) sommets, on peut se demander si la formule est vraie (réponse « oui ») ou fausse (réponse « non » ). Une formule pose donc un problème de décision : un graphe donné vérifie-t-il la formule ?
Remarquons que certaines formules posent des questions très simples, comme \(∀u\) \(∃v\) \(u\) \(→\) \(v\) qui est toujours vraie (car de chaque sommet sort une arête), \(∀u\) \(∃v\) \(∃w\) \((u → v)\) \(∧\) \((u → w)\) \(∧\) \(¬\)\((v = w)\) qui est toujours fausse (car dans les graphes que nous considérons, de chaque sommet sort exactement une arête), ou
\(∃u\) \(∃v\) \(∃w\) \(¬\)\((u = v)\) \(∧\) \(¬\)\((v = w)\) \(∧\) \(¬\)\((u = w)\) qui est vraie pour tous les graphes comportant au moins trois sommets. De telles formules présentent peu d’intérêt et sont qualifiées de triviales (techniquement, ce sont les formules qui sont vérifiées seulement par un nombre fini de graphes, ou qui ne sont pas vérifiées seulement par un nombre fini de graphes).
La complexité du point de vue des ordinateurs
Pour la science informatique, résoudre un problème consiste à écrire un programme qui fait le travail à notre place. Et, en bon(ne) informaticien(ne), on souhaite souvent écrire le programme le plus efficace possible, ici en termes de temps de calcul. Pour chaque formule on souhaite donc trouver le programme le plus rapide qui résout le problème de décision correspondant. Les différents problèmes sont plus ou moins complexes à résoudre : le programme le plus performant prendra plus ou moins de temps. Remarquons que pour les très petits graphes, on pourra facilement trouver la réponse « oui » ou « non » à n’importe quelle formule. La complexité apparaît pour les graphes de grande taille, c’est pour cela que l’efficacité est mesurée comme une fonction de la taille du graphe qui est donnée au programme. Sur la base d’une taille \(x = 100\), en doublant la taille du graphe (\(x = 200\)), un programme de complexité linéaire (\(x\)) prendra deux fois plus de temps, un programme de complexité quadratique (\(x\)2) prendra quatre fois plus de temps, un programme de complexité cubique (\(x\)3) prendra huit fois plus de temps, et un programme de complexité exponentielle (\(2\)\(x\)) prendra plus d’un milliard de milliards de milliards de fois plus de temps. Lorsque \(x\) devient l’exposant, le changement est drastique.
On classe ainsi les problèmes en deux grandes familles : P et EXP. Dans P on place ceux pour lesquels il existe un programme de complexité polynomiale (c’est-à-dire linéaire, quadratique, cubique, etc), et dans EXP ceux pour lesquels le meilleur programme est de complexité exponentielle (note de l’auteur : si vous connaissez la théorie de la complexité, vous verrez que j’abuse en parlant de EXP pour désigner EXP\P. Et vous verrez que j’abuse encore plus en oubliant les classes superpolynomiales et sous-exponentielles…). Les problèmes de la classe P sont résolus par des programmes efficaces, alors que les problèmes de la classe EXP sont résolus uniquement par des programmes inefficaces. Ceci a de grandes conséquences en pratique, car on peut résoudre les premiers à l’aide des ordinateurs, mais pas les seconds (techniquement on peut, mais cela prendrait beaucoup trop de temps). Et c’est à ce moment que les théoricien(ne)s de la complexité sont dans l’embarras, car il faut avouer que pour de nombreux problèmes nous ne savons pas s’ils appartiennent à la classe P ou à la classe EXP (malgré d’énormes efforts depuis 50 ans). Néanmoins, des outils mathématiques ingénieux ont été développés pour décrire toute une hiérarchie supposée de complexité entre P et EXP, et y classer les problèmes que l’on ne sait pas classer avec certitude dans P ou EXP. On a ainsi les emblématiques classes de problèmes NP-difficiles et coNP-difficiles, qui contiennent des problèmes dont la communauté scientifique pense en majorité qu’ils ne peuvent pas être résolus par des algorithmes de complexité polynomiale. Il s’agit de la fameuse question ouverte de savoir si les classes P et NP sont bien différentes, avec un million de dollars offert à qui prouvera ou réfutera cette conjecture (voir les références bibliographiques [1] et [3] ainsi que l’article Interstices sur la théorie de la complexité algorithmique pour plus de détails).
Alors, qu’a-t-on démontré au juste ?
Pour chaque formule exprimée en logique du premier ordre, le problème de décision associé demande, étant donné un circuit booléen encodant un graphe dont exactement une arête sort de chaque sommet, si ce graphe vérifie ou non la formule. Avec Guilhem Gamard, Pierre Guillon et Guillaume Theyssier, nous avons démontré que pour toute formule non triviale, le problème associé est très difficile : NP-difficile ou coNP-difficile (voir la référence [2]). Autrement dit pour chaque formule, soit elle est triviale et il existe un programme qui la résout en temps constant, soit elle n’est pas triviale et alors on ne connaît actuellement que des programmes extrêmement lents et on pense qu’il n’existe aucun programme efficace pour la résoudre.
Intuitivement, ce résultat dit que tout ce qui n’est pas trivial est complexe. Il faut néanmoins souligner que le « tout » fait référence aux questions portant sur l’ensemble des processus modélisés par des lois déterministes. Et le « complexe » porte sur la résolution exacte, à l’aide d’un programme qui donnerait toujours la bonne réponse avec une garantie stricte sur le temps de calcul. Pour n’importe quel programme supposé résoudre efficacement un problème donné, la démonstration de ce résultat explique comment construire des graphes (plus précisément leurs circuits booléens) qui mettront en déroute ledit programme.
Pour aller plus loin, nous travaillons maintenant à étendre ce résultat aux graphes modélisant des processus non déterministes, c’est-à-dire qui peuvent avoir zéro, une ou plusieurs arêtes qui sortent de chaque sommet. Pour \(n\) sommets, les circuits booléens ont alors \(2\) \(·\) \(log\)2(\(n\)) entrées et une seule sortie, qui calcule pour chaque paire de sommets (dont chacun est encodé par son numéro sur \(log\)2(\(n\)) bits, placés sur les entrées), s’ils sont reliés par une arête (sortie \(1\)), ou non (sortie \(0\)). Une seconde direction d’extension concerne la prise en compte de logiques plus expressives, car au premier ordre (lorsque \(∃\) et \(∀\) portent uniquement sur les sommets du graphe) certaines questions ne peuvent pas être formulées (il est par exemple impossible de demander si le graphe peut être séparé en deux parties déconnectées l’une de l’autre). Enfin, il serait tout aussi pertinent d’étudier d’autres notions de complexité, comme par exemple en autorisant les programmes à avoir une marge d’erreur aussi petite que possible, ou en demandant que le temps de réponse moyen soit optimisé.
En conclusion, il est impossible de comprendre tout parfaitement et sans grand effort dans le monde qui nous entoure (sous l’hypothèse P \(≠\) NP). Ce n’est peut-être pas une surprise, mais le démontrer dans une formulation mathématico-informatique est une aventure très enthousiasmante mêlant les domaines de la logique et de la complexité, dont nous ne sommes qu’au début !
- [1] Institut de mathématiques Clay. Sept problèmes du millénaire.
- [2] Guilhem Gamard, Pierre Guillon, Kevin Perrot, and Guillaume Theyssier. Rice-Like Theorems for Automata Networks. In STACS’2021, volume 187 of LIPIcs. Schloss Dagstuhl, 2021..
- [3] Sylvain Perifel. Complexité algorithmique. Ellipses, 2014.
Newsletter
Le responsable de ce traitement est Inria. En saisissant votre adresse mail, vous consentez à recevoir chaque mois une sélection d'articles et à ce que vos données soient collectées et stockées comme décrit dans notre politique de confidentialité
Niveau de lecture
Aidez-nous à évaluer le niveau de lecture de ce document.
Votre choix a été pris en compte. Merci d'avoir estimé le niveau de ce document !

Kévin Perrot
Enseignant-chercheur au Laboratoire d'Informatique et Systèmes (LIS) d'Aix-Marseille Université.
