Un joli algorithme géométrique et ses vilains problèmes numériques

Un petit dessin valant mieux qu’un grand discours, voilà ce que l’on cherche à faire :

L’enveloppe convexe peut être utilisée par exemple dans le cas suivant : si on a une antenne radio qui doit couvrir un certain nombre de points, on va chercher la meilleure place pour positionner cette antenne. Cela revient à trouver la plus petite ellipse contenant les points. Comme cette ellipse est convexe, il est clair que seuls les points de l’enveloppe convexe vont jouer un rôle. Calculer cette enveloppe permet donc d’éliminer rapidement un certain nombre de points non pertinents avant de chercher l’ellipse.

Par ailleurs, l’enveloppe convexe dans le plan est également un bon exemple d’autres configurations plus compliquées, pour lesquelles les mêmes problèmes que ceux décrits ici se posent.

Pour parvenir au résultat recherché, il faut maintenant expliquer à la machine la recette, c’est-à-dire l’algorithme.

Un exemple de construction : l’algorithme de la ficelle

Cette méthode, appelée aussi algorithme de Jarvis, va chercher à construire l’enveloppe convexe en débutant à un point dont on est sûr qu’il est sur l’enveloppe convexe, puis en recherchant le point suivant, jusqu’à ce que l’on ait fait tout le tour. Ainsi, on a construit un polygone en attachant une ficelle à un premier point, puis en emballant le paquet de points avec cette ficelle.

Plus précisément :

1. on va démarrer par le point le plus bas u
2. si p est le dernier point que l’on a construit, on va chercher le point q tel que la droite pq laisse tous les autres points sur sa gauche. q est le prochain point sur l’enveloppe. Si q = u on a fini, sinon on recommence l’étape 2.

En fait, pour trouver le point q tel que « la droite pq laisse tout les autres points sur sa gauche » l’ordinateur les essaie tous un à un en gardant le meilleur qu’il ait examiné.

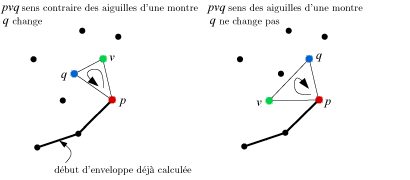
Pour savoir si un point v est meilleur que le point q, plusieurs solutions s’offrent à nous. Il est possible de comparer l’angle entre le dernier côté de l’enveloppe convexe et les deux côtés candidats pq et pv, mais on préfère en général regarder si le triangle pvq tourne ou non dans le sens des aiguilles d’une montre. Si pvq tourne dans le sens inverse des aiguilles d’une montre, alors v est meilleur que q et va le remplacer.

Principe de construction de l’enveloppe convexe par l’algorithme de la ficelle. Dans l’animation ci-dessus à droite, l’enveloppe convexe en construction est en noir, le dernier point construit p est en rouge, le meilleur candidat pour son successeur q est en bleu, et le nouveau point testé v est en vert.

Nous vous proposons une applet pour visualiser le déroulement de l’algorithme sur les exemples de votre choix.

Passons à une description plus proche du langage de programmation d’un ordinateur, ce qu’on appelle pseudo-code. La première partie du pseudo-code a pour but de trouver le point u, le point le plus bas. La deuxième partie construit l’enveloppe en passant en revue tous les points.

entrée : S un ensemble de points.

q ← le premier point de S
Pour tout v ∈ S après q
   si yv < yq alors q ← v ;
u ← q
p ← q
Répéter
   q ← le premier point de S
   Pour tout v ∈ S après q
      si pvq tourne dans le sens contraire des aiguilles d'une montre alors q ← v ;
   p.suivant ← q ;
Tant que p ≠ u

Prédicats

Dans le pseudo-code de l’algorithme de Jarvis, il y a une partie dite combinatoire, dans laquelle on s’occupe de l’organisation des points, et une partie où on regarde vraiment la position géométrique des choses. Ces petits calculs géométriques, à partir desquels l’ordinateur prend des décisions, on les appelle des prédicats. Ici, il s’agit de savoir dans quel sens tourne pvq.

Comment cette question peut-elle être transcrite pour l’ordinateur ? Regardons notre prédicat :

« pvq tourne dans le sens contraire des aiguilles d’une montre ».

Il peut être écrit d’une façon plus mathématique de plusieurs manières. Par exemple, nous pouvons adopter celle-ci :

(x_q-x_p)(y_v-y_p)-(x_v-x_p)(y_q-y_p) < 0

où x_p et y_p sont les coordonnées du point p, x_q et y_q celles de q, x_v et y_v celles de v.

On voit ici que notre prédicat repose sur un calcul numérique, fait sur des nombres. Les calculs faits par les ordinateurs utilisent soit des nombres entiers, soit des nombres à virgule flottante dits « flottants » (en anglais floating-point numbers, ou en abrégé « float »), ces derniers sont arrondis. Si on utilise des nombres flottants, ce calcul aura donc une certaine imprécision. Dans la plupart des cas, ce n’est pas très grave, car on ne s’intéresse qu’au signe de la valeur calculée, et une petite erreur ne changera en général pas le signe.

Malheureusement, si les points sont presque alignés, la valeur calculée sera très petite, et une petite imprécision risque de changer le signe. Et, plus grave que cette imprécision, nos résultats peuvent être incohérents entre eux, ce qui va emmener notre algorithme dans des cas non prévus, qui vont le perturber gravement.

Exemples d’erreur dans le prédicat

Vérifions à partir d’un exemple que lorsque des points sont presque alignés, le calcul peut amener à se tromper sur le signe du résultat et sur l’orientation du triangle.

Prenons tout d’abord un exemple de points très grossièrement presque alignés, avec les coordonnées suivantes pour les points p, q et v :
p = (0.5, 0.5), q = (12, 13), v = (24, 24)

Le calcul pas à pas donne le résultat suivant :
(x_q-x_p)(y_v-y_p)-(x_v-x_p)(y_q-y_p)
= (12 – 0.5) (24-0.5) – (24 – 0.5) (13 – 0.5)
= 11.5 x 23.5 – 23.5 x 12.5
= 270.25 – 293.75
= – 23.5

Le résultat est négatif, cela signifie que le triangle vqp tourne dans le sens contraire des aiguilles d’une montre.

Prenons maintenant des points finement presque alignés :
p = (0.5000029, 0.5000027), q = (12, 12), v = (24, 24)

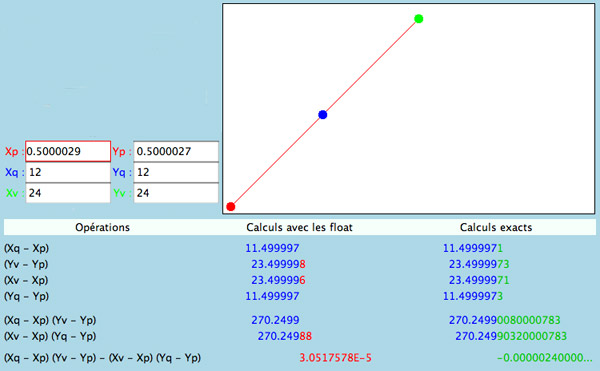
Pour le calcul, le point p est converti de décimal en binaire, avec des nombres flottants ayant 24 chiffres binaires significatifs. Sa valeur écrite en décimal est alors plus proche de v = (0.500002920628, 0.500002682209)

On fait le calcul pas à pas :
(x_q-x_p)(y_v-y_p)-(x_v-x_p)(y_q-y_p)
= (12 – 0.500002920628) (24 – 0.500002682209) – (24 – 0.500002920628) (12 – 0.500002682209)
= 11.499997139 x 23.4999980927 – 23.4999961853 x 11.499997139
= 270.249908447 – 270.24987793
= 0.000030517578125

Ici, les erreurs initiales qui portent sur y_v-y_p et x_v-x_p se propagent.

Le même calcul, refait avec plus de précision, donne un résultat de signe opposé :
(x_q-x_p)(y_v-y_p)-(x_v-x_p)(y_q-y_p)
= (12 – 0.500002920628) (24 – 0.500002682209) – (24 – 0.500002920628) (12 – 0.500002682209)
= 11.4999970794 x 23.4999973178 – 23.4999970794 x 11.4999970794
= 270.24990052 – 270.249903381
= – 0.00000286102294922

Nous vous proposons une applet pour visualiser les calculs correspondant à ces exemples et à d’autres de votre choix.

Exemples d’incohérence

Les problèmes rencontrés au niveau du prédicat ont des conséquences sur le déroulement de l’algorithme. Ils peuvent même le faire « boucler », c’est-à-dire ne jamais se terminer.

Voici un exemple avec quatre points alignés que notre algorithme ne sait pas résoudre :
w₁ = (12,12), w₂ = (24,24), w₃ = (0.5, 0.5), w₄ = (30, 30)

Dans ce cas, pour certaines implémentations de l’algorithme, cela peut boucler, parce que les cas particuliers où 3 points sont alignés ne sont pas gérés. Il faudrait modifier le pseudo-code en remplaçant la ligne :

si pvq tourne dans le sens contraire des aiguilles d'une montre alors q ← v

par :

si pvq tourne strictement dans le sens contraire des aiguilles d'une montre alors q ← v
si pvq alignés et q entre p et v alors q ← v.

Mais cela ne va pas suffire à résoudre les problèmes. Prenons maintenant un exemple où les 4 points sont presque alignés :
w₁ = (0.5000029, 0.5000027), w₂ = (12,12), w₃ = (24, 24), w₄ = (30, 30.000001)

Dans cet exemple, le calcul reste très faux, car le point w₄ est complètement oublié. Le problème correspond à l’erreur de prédicat évoquée précédemment.

En effet, quand w₃ est le point rouge p, que w₁ est le point bleu q et que w₄ est le nouveau point testé v (en vert), le triangle pvq est évalué comme tournant dans le sens des aiguilles d’une montre, ce qui conduit à tort à éliminer v = w₄.

Cet exemple est appelé « Dysfonctionnement 1 » dans l’applet illustrant le fonctionnement de l’algorithme.

De telles circonstances peuvent amener des erreurs grossières dans le calcul de l’enveloppe, même lorsqu’il y a des points qui ne sont pas presque alignés. C’est ce que montrent les exemples « Dysfonctionnement 2 » et « Dysfonctionnement 3 » où d’autres points sont ajoutés.

Les solutions

Trouver des solutions à ces problèmes est actuellement un domaine de recherche actif.

La solution la plus courante consiste à se passer du calcul avec des nombres flottants pour utiliser du calcul exact. Malheureusement, le calcul exact est beaucoup plus coûteux (en temps de calcul) que le calcul flottant. On cherche donc à mettre au point des solutions alliant la rapidité du calcul flottant à la fiabilité du calcul exact. Sur ce sujet, vous pouvez lire le document Des arithmétiques pour la géométrie.