Voulez-vous vraiment toutes les réponses ?
En donnant quelques mots en entrée à votre moteur de recherche, celui-ci renvoie une immense quantité de pages internet pertinentes. Produire ainsi de nombreuses réponses à partir d’une simple entrée, c’est le domaine des algorithmes d’énumération que nous présentons ici. C’est un peu le contraire de l’apprentissage en intelligence artificielle (IA) qui utilise d’énormes masses de données en entrée, typiquement des millions de photos annotées, pour ensuite être capable de répondre à une question comme « est-ce que cette photo représente un chat ? ». Nous allons d’abord donner quelques exemples pour illustrer le concept de problèmes d’énumération et son intérêt. La plupart de ces exemples sont modélisés par des graphes, car ce sont des problèmes simples et facilement visualisables, mais on rencontre aussi énormément de problèmes d’énumération dans les bases de données, en logique, en bio-informatique, en cryptographie…
Un premier exemple, familier si vous utilisez une application pour trouver votre itinéraire est de résoudre un problème du type « comment faire le trajet Strasbourg-Toulouse ? ». Ce problème correspond à la recherche d’un chemin dans un graphe. Un graphe est un ensemble de sommets, ici les villes, et d’arêtes entre deux sommets, ici les routes entre deux villes. On associe souvent à chaque arête un poids qui représente ici la longueur de la route représentée par l’arête. Un chemin dans un graphe est une suite de sommets reliés par des arêtes. On cherche généralement le plus court chemin entre deux sommets.
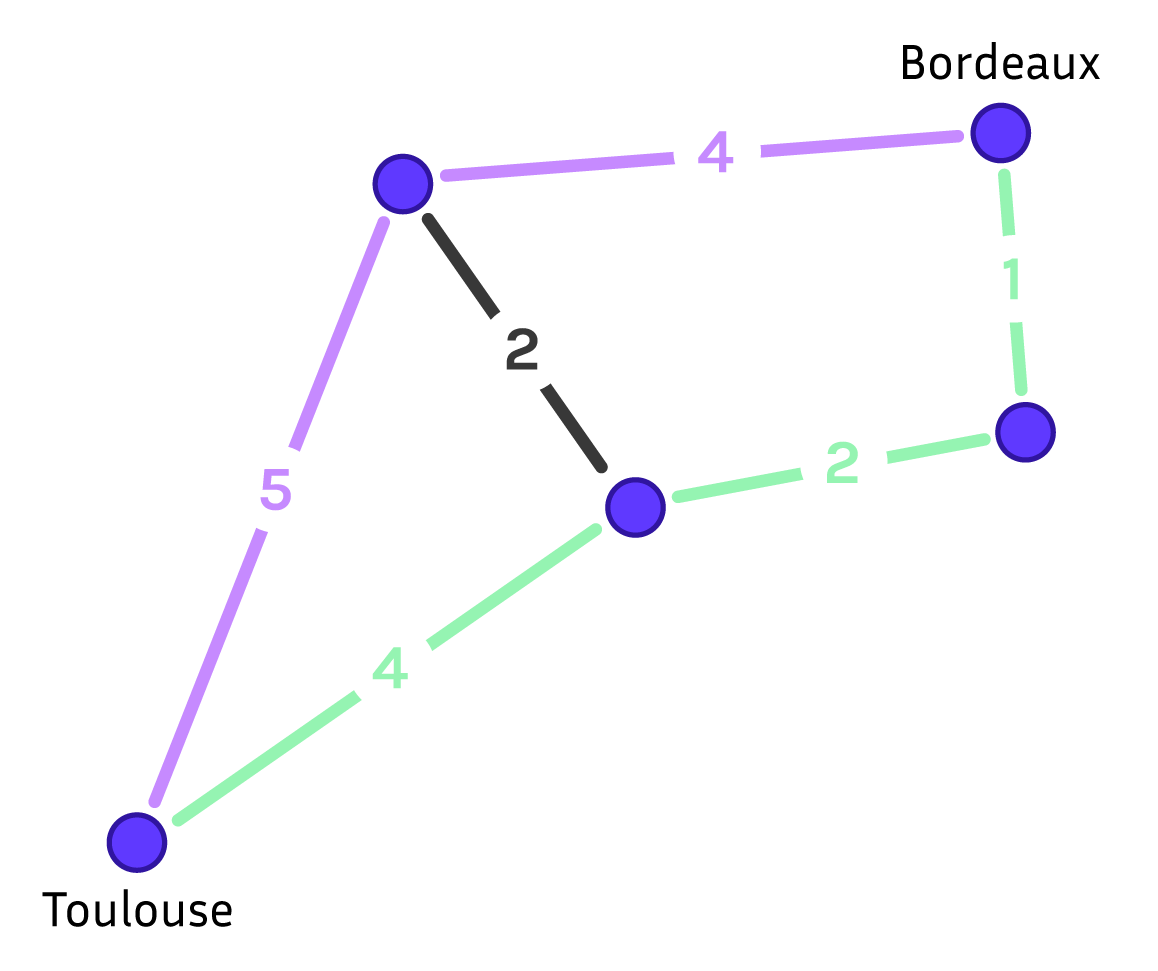
Un graphe routier avec cinq villes. Schéma réalisé par Sacha Berna.
Sur le graphe ci-dessus, le chemin en vert est de longueur \(7 = 1 + 2 + 4\), il est plus court que le chemin en violet de longueur \(9\) et c’est le plus court chemin entre Strasbourg et Toulouse. Si vous voulez savoir s’il existe un chemin entre deux villes, il s’agit d’un problème de décision. Si vous voulez obtenir ce chemin, il s’agit d’un problème de recherche et si vous voulez uniquement le plus court, il s’agit d’un problème d’optimisation. Dans notre cas, l’application fournit plusieurs itinéraires possibles, elle a donc résolu le problème d’énumérer les chemins entre Strasbourg et Toulouse. Pour ne pas vous inonder avec les milliards de trajets existants, l’application se contente de ne montrer que quelques trajets avec un temps de parcours raisonnable.
Un problème d’énumération plus complexe est étudié dans les réseaux sociaux : la détection de communauté. Un réseau social est représenté par un graphe dont les sommets sont les utilisateurs et une arête entre deux sommets correspond à deux personnes qui ont interagi. Pour structurer ce grand nombre d’utilisateurs et interpréter le réseau, on aime détecter des communautés. La définition la plus simple de communauté, qu’on va utiliser ici, est un ensemble d’utilisateurs qui ont tous interagi les uns avec les autres. Ils forment dans le graphe ce que l’on appelle une clique ou un sous-graphe complet. L’objectif est de générer toutes ces communautés. Pour limiter le nombre de solutions produites, on se restreint aux communautés maximales, c’est-à-dire celles qui ne sont pas contenues dans une communauté plus grande. C’est le problème théorique, très étudié, de la recherche des cliques maximales. Dans le graphe ci-dessous, Ana, Bilal et Clémentine forment une clique de taille \(3\), elle est maximale, car on ne peut ajouter Dina ou Émile qui ne sont pas connectés à Ana.
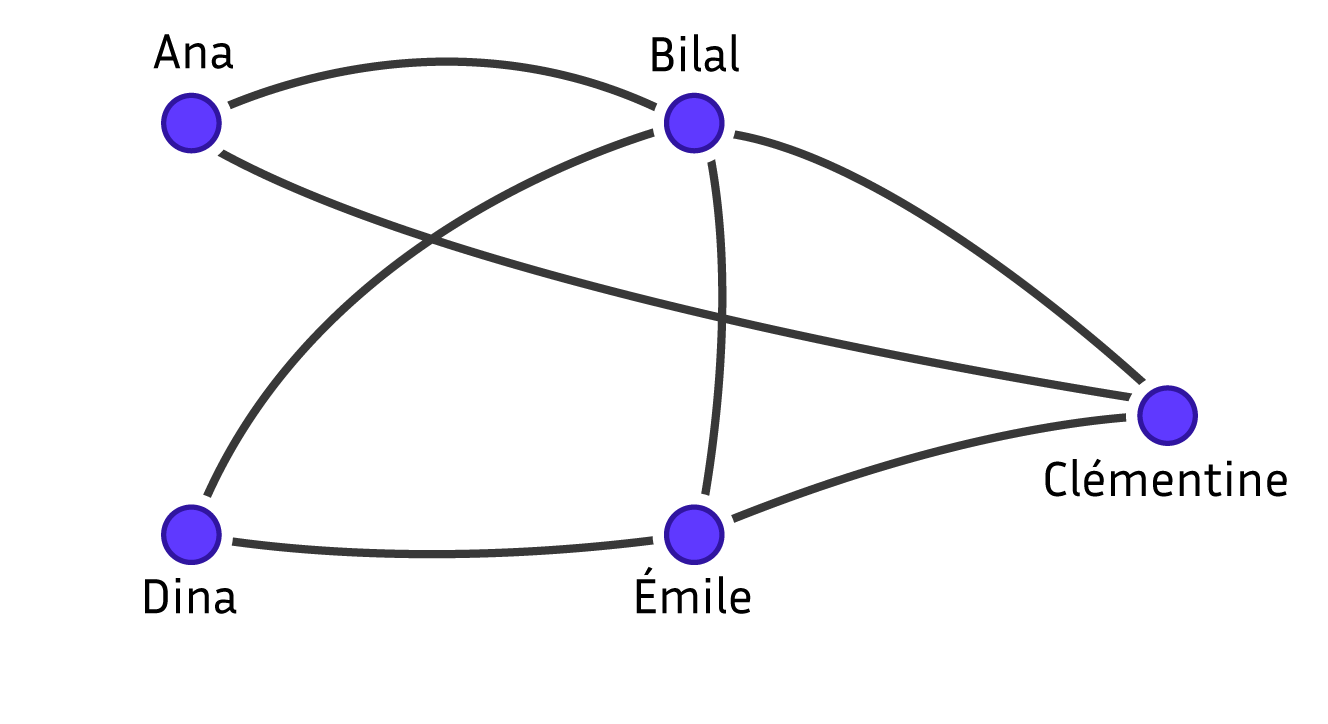
Un réseau social de cinq individus. Schéma réalisé par Sacha Berna.
Certains problèmes d’énumération ont été étudiés bien avant les réseaux sociaux et même les ordinateurs.

Hexagramme 35 du Yi Jing. Crédit : Ben Finney, Attribution, via Wikimedia Commons.
Un Hexagramme est une suite de 6 lignes continues (yang) ou discontinues (yin), ils sont présentés dans le livre du Yi King pour faire de la divination. Le problème d’énumération consiste à lister tous les hexagrammes sans en oublier, ni les répéter. Il a été résolu par la méthode de Fu Hsi, il y a plus de 3000 ans. Ce problème revient à donner les 64 premiers entiers en base deux. Vous connaissez en fait le même type d’algorithme d’énumération depuis la maternelle : compter en base 10. Il s’agit de résoudre le problème suivant : étant donné un entier \(N\), écrire dans l’ordre tous les entiers de \(0\) à \(N\). L’algorithme qui permet de produire ces nombres commence avec l’entier \(0\) et ajoute \(1\) répétitivement jusqu’à atteindre \(N\).
Maintenant qu’on a donné quelques exemples de problèmes d’énumération, on peut se demander pourquoi on veut résoudre de tels problèmes. La première application est le comptage : si on veut savoir combien d’objets d’un certain type existent, il faut souvent les générer exhaustivement. On peut par exemple compter toutes les manières de positionner huit reines sur un échiquier sans qu’elles se menacent mutuellement. Par ailleurs, il est intéressant de générer l’ensemble de toutes les solutions possibles quand le critère de choix parmi les solutions n’est pas connu a priori et peut varier. Par exemple, quand vous générez les trajets Strasbourg-Toulouse, vous ne savez pas si l’utilisateur veut minimiser son temps de déplacement, le coût du trajet, la pollution ou encore passer par Grenoble pour aller voir sa grand-mère. Enfin, pour résoudre un problème d’optimisation, c’est-à-dire trouver la meilleure solution pour un critère bien défini, on peut lister toutes les solutions et retenir celle qui maximise notre critère. Par exemple, je veux trouver le plus court chemin entre Toulouse et Strasbourg qui passe par Bordeaux, Lyon et Marseille. Ce problème est un problème NP-complet, équivalent au problème du voyageur de commerce, ce qui veut dire qu’il n’y a pas d’algorithme efficace connu pour le résoudre. La technique la plus simple est de lister les \(n!\) chemins, où \(n\) est le nombre de villes de la carte, et de choisir le plus court. Néanmoins, on peut se contenter de ne lister que des chemins intéressants : entre chaque paire de villes par lesquelles on doit passer, on calcule un plus court chemin, ce qui est rapidement calculable. On obtient alors une carte avec uniquement les \(k\) villes par lesquelles on est obligé de passer et on peut lister les \(k!\) chemins de cette carte.
Dans notre exemple, il faut décider dans quel ordre on va visiter les trois villes intermédiaires, c’est-à-dire lister les 6 permutations à trois éléments :
| – Bordeaux, Lyon, Marseille : | 2219 = 945 + 556 + 314 + 404 |
| – Bordeaux, Marseille, Lyon : | 2443 = 945 + 646 + 314 + 538 |
| – Lyon, Bordeaux, Marseille : | 2094 = 488 + 556 + 646 + 404 |
| – Lyon, Marseille, Bordeaux : | 1692 = 488 + 314 + 646 + 244 |
| – Marseille, Bordeaux, Lyon : | 2544 = 804 + 646 + 556 + 538 |
| – Marseille, Lyon, Bordeaux : | 1918 = 804 + 314 + 556 + 244 |
|
|
Strasbourg |
Toulouse |
Bordeaux |
Lyon |
Marseille |
|
Strasbourg |
0 |
970 |
945 |
488 |
804 |
|
Toulouse |
970 |
0 |
244 |
538 |
404 |
|
Bordeaux |
945 |
244 |
0 |
556 |
646 |
|
Lyon |
488 |
538 |
556 |
0 |
314 |
|
Marseille |
804 |
404 |
646 |
314 |
0 |
C’est seulement une fois calculée la longueur de tous les trajets qu’on peut conclure que le plus court est celui passant par Lyon puis Marseille et enfin Bordeaux. Si je veux mettre en place un parcours touristique passant par 20 lieux remarquables, il faut alors considérer 20! = 2.432.902.008.176.640.000 chemins, ce qui est impossible même pour votre ordinateur.
Les Méthodes Algorithmiques
Il existe deux familles de méthodes pour résoudre les problèmes d’énumération, le partitionnement et le supergraphe. Nous allons les présenter pour le problème de détection de communauté, en se limitant à la recherche des communautés de taille trois, c’est-à-dire les triangles d’un graphe.
La méthode de partitionnement essaye de découper l’ensemble des communautés en plusieurs morceaux disjoints. Pour ce faire, on sélectionne un individu particulier de notre graphe, disons Émile, qui va servir à couper l’ensemble des communautés en deux : celles qui contiennent Émile et celles qui ne le contiennent pas. Ces deux ensembles n’ont pas de communautés en commun et on peut donc les construire indépendamment. Les communautés de taille trois qui contiennent Émile sont les communautés de taille deux dans le graphe des personnes en relation avec Émile. Une communauté de taille deux est simplement un ensemble de deux personnes reliées par une arête. Il suffit donc de lister les arêtes du graphe des personnes en relation avec Émile pour obtenir ces communautés. Les communautés de taille trois sans Émile sont les communautés de taille trois dans le graphe dont on a retiré Émile. On peut les trouver en appliquant de nouveau notre algorithme à ce graphe plus simple, en choisissant maintenant un autre individu pour faire notre partition, disons Clémentine, et on continue de la même manière.
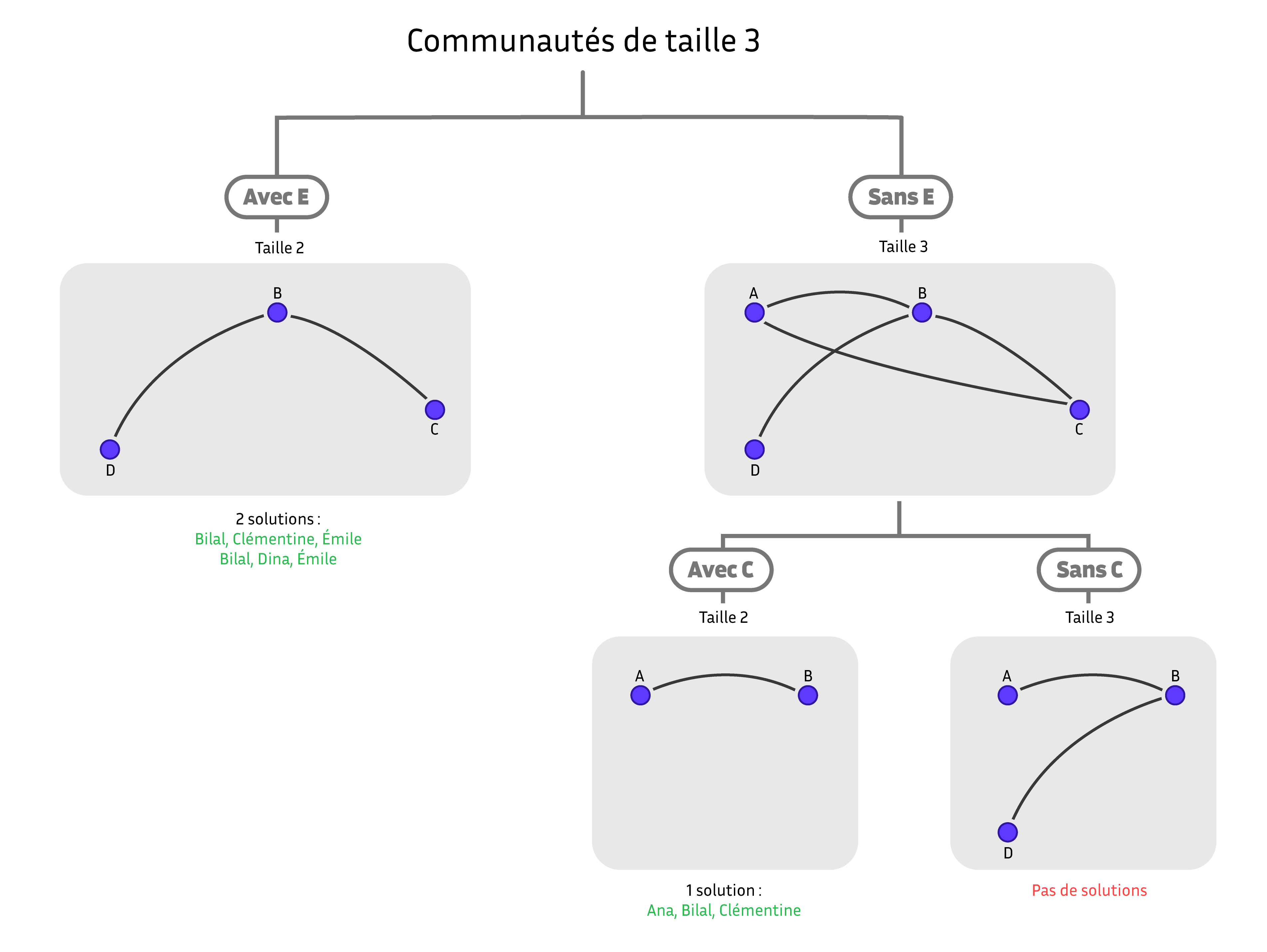
Exécution du partitionnement binaire. Les individus sont donnés par leur initiale. Schéma réalisé par Sacha Berna.
Une méthode de partitionnement alternative est basée sur la construction élément par élément des communautés. On va générer tous les triplets d’individus en vérifiant qu’ils forment une communauté. On choisit le premier individu parmi tous les individus possibles. Pour respecter la contrainte de construire une communauté, on choisit un deuxième élément dans les voisins du premier élément et enfin un troisième élément parmi les voisins du premier et du deuxième. Cette méthode a un gros défaut, elle va générer chaque communauté dans tous les ordres possibles de ses membres. Par exemple, on produit la séquence (Ana, Bilal, Clémentine) mais aussi (Bilal, Clémentine, Ana). C’est un problème courant en énumération, on génère des solutions redondantes et il faut trouver un moyen de les éliminer. Pour résoudre ce problème dans cet algorithme, on définit une représentation canonique des solutions : on ne produit que les séquences de trois personnes dans l’ordre alphabétique croissant. On va donc obtenir (Ana, Bilal, Clémentine) mais pas (Bilal, Clémentine, Ana). Dans l’algorithme précédent, cela veut dire que quand on sélectionne un élément, on doit ensuite se restreindre à ses voisins qui sont plus grands dans l’ordre alphabétique.
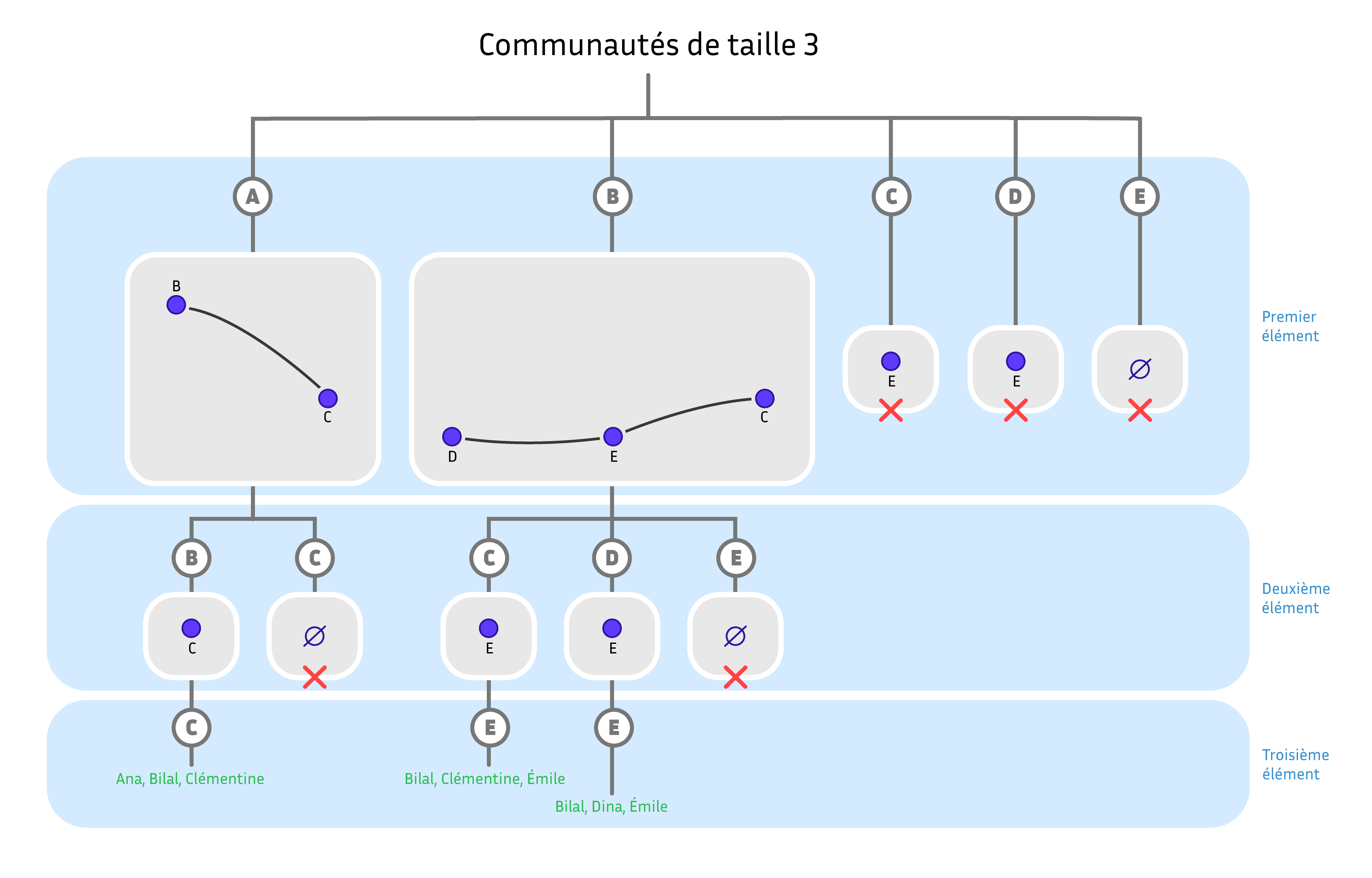
Représentation de l’algorithme de partitionnement générant des triplets canoniques. Chaque nœud interne de l’arbre représente un graphe dans lequel on doit trouver des cliques plus petites pour compléter les sommets déjà choisis. Quand on ne peut pas étendre un ensemble de sommets en une clique de la taille recherchée, la branche est coupée. Schéma réalisé par Sacha Berna.
La deuxième méthode, appelée méthode du supergraphe nécessite de définir une relation de proximité entre deux communautés. Deux communautés \(X\) et \(Y\) sont en relation si on peut passer de \(X\) à \(Y\) de la manière suivante. On ajoute à \(X\) un élément \(y\) membre de \(Y\). Puis comme on veut une communauté, on va enlever tous les éléments de \(X\) qui ne sont pas reliés à \(y\). Si nécessaire, on fait ensuite grossir la communauté en y ajoutant des éléments dans l’ordre alphabétique jusqu’à ce qu’elle soit de taille trois. Sur la figure ci-dessous, on voit qu’on peut passer de la solution (Ana, Bilal, Clémentine) à la solution (Bilal, Clémentine, Émile) en ajoutant Émile.
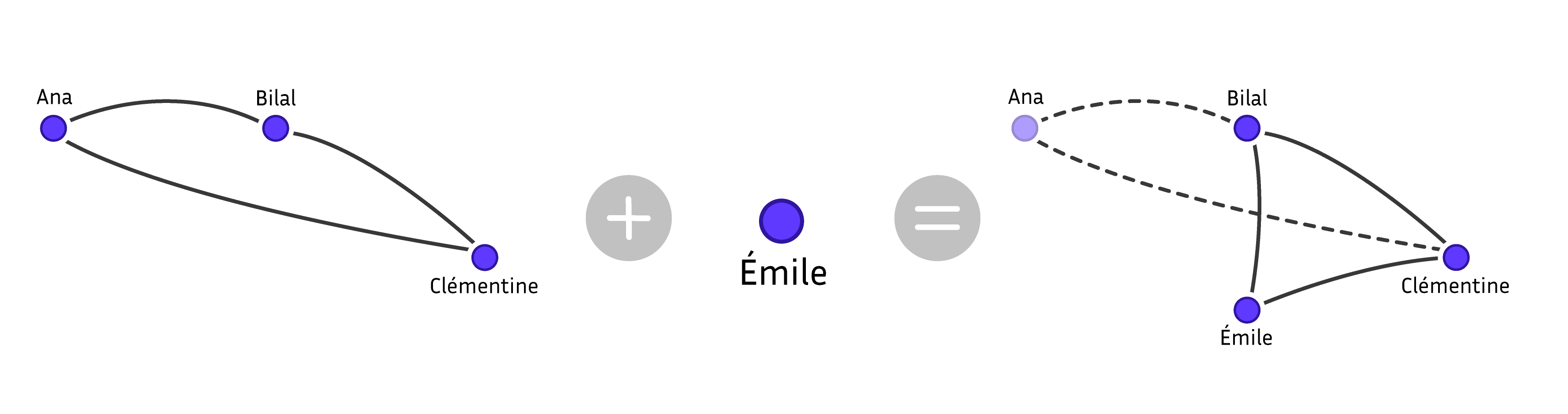
Schéma réalisé par Sacha Berna.
Cette relation de proximité définit un graphe orienté sur toutes les communautés de taille trois, qu’on appelle le supergraphe : chaque communauté est un sommet de ce graphe et il y a un arc entre \(X\) et \(Y\) si on peut passer de \(X\) à \(Y\) par la relation de proximité. Si le supergraphe est fortement connexe, c’est-à-dire qu’il y a un chemin entre n’importe quelle paire de communautés, alors on peut toutes les générer en parcourant le supergraphe. Le supergraphe de notre exemple contient tous les arcs possibles donc il est fortement connexe. Par contre, si le supergraphe n’est pas fortement connexe, on peut essayer de trouver un petit ensemble de sommets à partir desquels on peut atteindre tous les éléments du supergraphe. Trouver une bonne relation de proximité afin que le supergraphe d’un problème donné soit fortement connexe, et proposer des méthodes pour prouver qu’un supergraphe est connexe à partir de certaines de ses propriétés est un sujet de recherche actuel très dynamique.
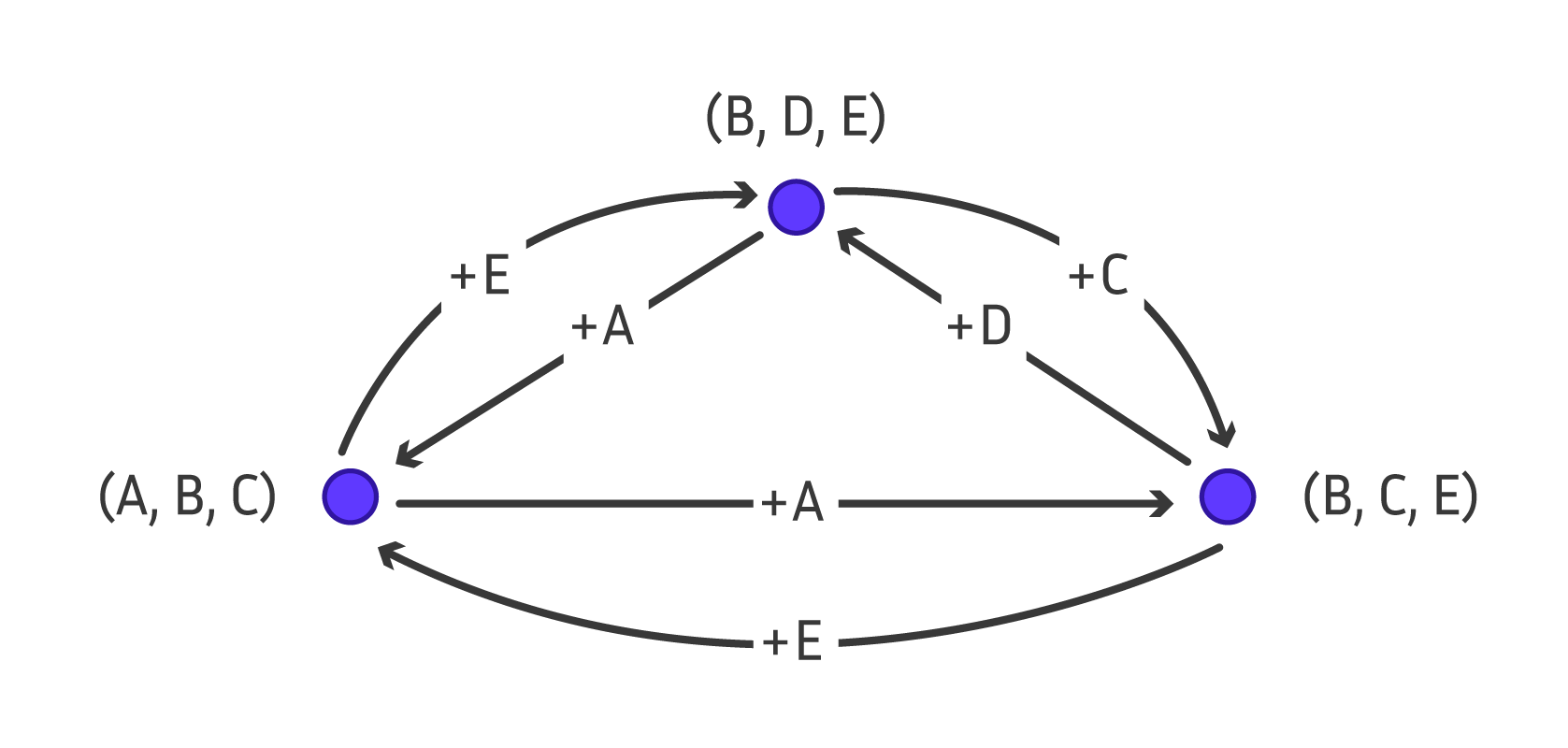
Supergraphe. Schéma réalisé par Sacha Berna.
Complexité : les Bons et les Mauvais Algorithmes
Pour évaluer l’efficacité d’un algorithme, comme celui qui cherche le plus court chemin entre Toulouse et Strasbourg, on veut évaluer le temps qu’il met pour trouver la solution. Si notre carte routière contient cinq villes ou cent, le temps de calcul ne sera pas le même. On s’intéresse à la complexité asymptotique, c’est-à-dire comment le temps de calcul augmente quand on augmente la taille de l’entrée. Si on multiplie le nombre de villes par deux et que le temps est multiplié par deux, on a un algorithme en temps linéaire. Si le temps est multiplié par deux quand on ajoute une seule ville à la carte, on a un algorithme en temps exponentiel, très inefficace. On considère qu’un algorithme est efficace s’il est en temps polynomial, c’est-à-dire qu’il y a un entier \(k\) (typiquement \(k\) vaut 1, 2 ou 3) tel que l’algorithme doit faire \(N^k\) opérations sur une entrée de taille \(N\). Autrement dit, si on double la taille de l’entrée, on multiplie le temps de calcul par \(2^k\). Par exemple, l’algorithme de Dijkstra permet de trouver le plus court chemin entre deux villes dans une carte avec \(N\) villes en temps \(N^2\), c’est donc un algorithme polynomial. Si on double la taille de la carte, l’algorithme de Dijkstra prendra \(4 = 2^2\) fois plus de temps à trouver un plus court chemin.
Le problème avec cette mesure d’efficacité pour les algorithmes d’énumération, c’est que les solutions peuvent être très nombreuses. Par exemple, dans un graphe avec \(N\) sommets, on peut avoir \(2^{N/3}\) communautés maximales. Donc, tous les algorithmes listant les communautés maximales prendront au moins un temps exponentiel de \(2^{N/3}\), simplement pour écrire toutes les solutions. On voudrait avoir des algorithmes plus rapides quand il y a peu de solutions, c’est ce qu’on appelle des algorithmes sensibles à la sortie. Les algorithmes dont le temps de calcul dépend uniquement de la taille de l’entrée sont appelés sensibles à l’entrée. Pour qu’un algorithme d’énumération soit considéré efficace, on demande que sur une entrée de taille \(N\) et une sortie de \(S\) solutions, il soit polynomial en \(N\) et \(S\). c’est-à-dire qu’on doit pouvoir produire les \(S\) solutions en temps \(N^kS^l\) où \(k\) et \(l\) sont des entiers. Par exemple, il y a un algorithme qui liste les communautés maximales dans un graphe à \(N\) sommets en temps \(N^3S\).
 |
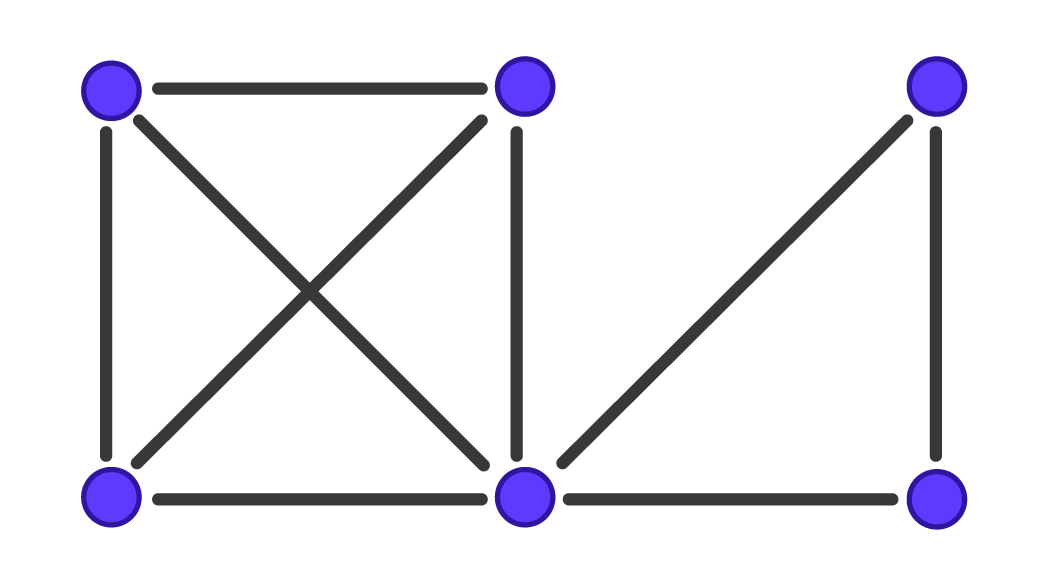 |
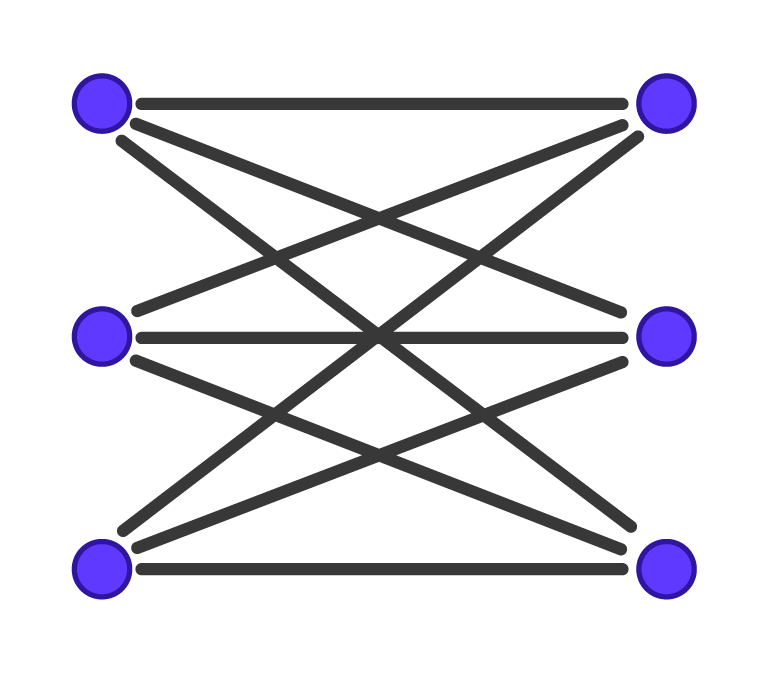
Représentation de deux graphes de taille six. Schémas réalisés par Sacha Berna. |
|
Dans le graphe de gauche, il y a 9 cliques maximales de taille 2. Dans le graphe de droite, il y a deux cliques maximales de taille 3 et 4. Ainsi, l’algorithme qui liste les cliques maximales sera 4,5 fois plus rapide sur le graphe de droite que sur le graphe de gauche alors que les deux graphes ont le même nombre de sommets.
Malheureusement, cette caractérisation de la complexité d’un algorithme d’énumération n’est pas pertinente quand il y a trop de solutions . En effet, même si votre algorithme est sensible à la sortie, rapide, mais que vous avez un nombre immense de solutions et qu’elles sont toutes produites à la fin du calcul, vous ne verrez jamais aucune solution. On préfère donc générer les solutions au fur et à mesure du déroulement de l’algorithme et pas en bloc à la fin. Cela correspond à notre usage d’un moteur de recherche, l’application donne 10 réponses et si nous ne sommes pas satisfaits, un clic sur un bouton produit les 10 réponses suivantes calculées à la volée, et cela, jusqu’à épuisement des réponses. On appelle le temps pour obtenir une nouvelle solution le délai de l’algorithme. On peut aussi mesurer le temps incrémental de l’algorithme qui est défini comme le temps nécessaire pour générer les \(K\) premières solutions. On considère qu’un algorithme est efficace si son temps incrémental est polynomial en la taille de l’entrée et du nombre de solutions à produire, ou mieux, si son délai est polynomial en la taille de l’entrée.
Les méthodes de partitionnement et de supergraphe ont un délai polynomial si elles vérifient certaines propriétés. La méthode de recherche de solutions par partitionnement peut créer un ensemble de solutions vide, ce qui est arrivé quand on a décidé de ne prendre ni Émile ni Clémentine dans notre exemple. Pour rendre la méthode efficace en fonction du nombre de solutions (sensible à la sortie), il faut éviter de partitionner inutilement un ensemble de solutions vide en plusieurs morceaux. Cela veut dire qu’on doit pouvoir détecter si un graphe contient une communauté de taille trois, ce qui est possible en temps polynomial. Si on considère le problème plus général d’énumérer les cliques maximales, détecter si un graphe contient une clique maximale avec certains éléments fixés est un problème NP-complet, donc le partitionnement n’est pas efficace.
La méthode d’énumération par parcours de supergraphe est à délai polynomial si, pour chaque solution, on peut trouver tous ses voisins en temps polynomial. Dans notre exemple de clique de taille trois, il suffit d’ajouter à une solution chacun des \(N\) sommets du graphe, de retirer les sommets incompatibles et de compléter avec les sommets restants. Chaque voisin est produit en temps \(N\) et on a \(N\) voisins, donc on produit bien tous les voisins d’une solution en temps polynomial \(N^2\). Contrairement à l’algorithme de partitionnement, cette méthode s’étend à la génération des cliques maximales, la difficulté étant de prouver que le supergraphe est toujours fortement connexe.
Submergé par les réponses ?
Pour répondre à la question posée par le titre, non vous ne voulez pas toutes les réponses. Par exemple, si je cherche « énumération » sur Google, le moteur de recherche me propose 4 370 000 résultats et je n’ai pas assez d’une vie pour tous les lire. Si un chimiste veut lister toutes les formes possibles de molécules organiques avec 30 atomes, il se retrouve avec des centaines de milliards de possibilités, qui sont même impossibles à stocker sur un ordinateur. Une direction de recherche prometteuse est donc d’imaginer des méthodes pour remplacer l’énumération exhaustive.
Imaginons qu’on veut calculer des statistiques sur l’ensemble de solutions, par exemple la taille moyenne d’une communauté maximale. Il suffit alors de donner un générateur qui produit une solution au hasard uniformément parmi toutes les solutions, ce que sait très bien faire la combinatoire énumérative. On peut ensuite utiliser la méthode du sondage : tirer un certain nombre de communautés maximales au hasard et calculer la moyenne de leurs tailles, qui approchera la moyenne réelle.
Quand les solutions sont fournies à un utilisateur humain pour interprétation, leur nombre doit être fortement limité. Pour maximiser l’utilité de ces solutions, il est intéressant de donner les solutions les plus différentes possibles. Par exemple, deux communautés maximales complètement disjointes donnent plus d’information sur un réseau social que deux communautés qui ne diffèrent que d’un membre. C’est l’approche des applications de calcul d’itinéraire qui vont plutôt donner des trajets très différents, par exemple un qui prend des autoroutes et l’autre des nationales. On utilise généralement la distance de Hamming entre deux solutions, définie comme le nombre de sommets qui sont dans une solution (un chemin ou une communauté) mais pas dans l’autre. Un ensemble de solutions diverses maximise la somme des distances de Hamming entre chacun de ses éléments. Malheureusement, les problèmes deviennent beaucoup plus complexes quand on veut des solutions diverses et ce qu’on gagne en efficacité en générant peu de solutions, on le perd en difficulté à garantir la diversité. Par exemple, trouver des chemins de taille donnée entre deux villes, en maximisant leur diversité est un problème NP-difficile. En effet, on peut utiliser un algorithme qui résout ce problème pour décider s’il existe \(k\) chemins disjoints de longueur exactement \(l\) entre deux sommets dans un graphe, ce qui est un problème NP-complet.
Enfin, on peut essayer de diminuer le nombre de solutions à lister en trouvant de la structure dans l’ensemble des solutions. Par exemple, si vous cherchez un trajet entre Jussieu et le MIT, vous aurez un voyage en trois parties : le trajet entre Jussieu et l’aéroport Paris CDG, le vol entre Paris et Boston, puis le trajet entre l’aéroport de Boston et le MIT. Il suffit alors de produire les solutions pour chacun de ces trois trajets indépendamment, ce qui fait beaucoup moins de trajets que leurs combinaisons.
Newsletter
Le responsable de ce traitement est Inria. En saisissant votre adresse mail, vous consentez à recevoir chaque mois une sélection d'articles et à ce que vos données soient collectées et stockées comme décrit dans notre politique de confidentialité
Niveau de lecture
Aidez-nous à évaluer le niveau de lecture de ce document.
Votre choix a été pris en compte. Merci d'avoir estimé le niveau de ce document !

