Variabilité, limite, stabilité en informatique
Il semble que rien ne bride la variabilité des technologies informatiques. Quiconque a dû choisir une version de Linux a pu en faire l’expérience devant la variété des distributions. Pourtant, on peut dire d’un logiciel qu’il « tourne sur Linux », comme s’il y avait un concept stabilisé de Linux. Les technologies informatiques les plus populaires sont ainsi le résultat d’une évolution très foisonnante qui peut malgré tout se résumer en un concept.
À un niveau beaucoup plus interne, certains algorithmes sont conçus comme des processus de stabilisation d’un calcul, et introduire de la variabilité dans les données est un moyen d’améliorer la qualité des résultats obtenus. En fait, pour peu qu’il soit itératif, c’est-à-dire presque tout le temps, un calcul peut être analysé comme la recherche d’un point fixe, une limite, dans le domaine des valeurs prises par les variables du calcul.
L’action de répéter une opération s’appelle une itération. C’est une composante essentielle de la programmation.
Le nombre de fois où l’opération est répétée peut être fixé avant de commencer l’itération ; c’est le cas de la boucle FOR.
Par exemple, pour répéter une opération pour toutes les valeurs de i allant de 1 jusqu’à n, on écrira :
for i=1 jqa n do ... od.
Ce nombre peut aussi ne pas être fixé a priori, mais dépendre de l’émergence d’une condition ; c’est le cas de la boucle WHILE (tant que en français).
La condition peut être externe, c’est-à-dire dépendre d’un acteur extérieur au programme.
Par exemple :
while pas de courrier do vérifier la boîte aux lettres od.
Elle peut aussi être interne, c’est-à-dire ne dépendre que des actions du programme.
Par exemple :
while ido augmenter i od.
Rappelons qu’un point fixe d’une fonction f est une valeur x telle que f(x) = x. Une fonction peut ne pas avoir de point fixe (par exemple, x → x+1 définie sur ℝ), n’en avoir qu’un (par exemple, x → x/2 définie sur ℝ), ou en avoir plusieurs (par exemple, x → y tel que y divise x et y n’a pas de diviseur).
Un exemple peut montrer une utilisation de cette notion. La fonction f : ℝ → ℝ, f(x) = 1/2(x + n/x), a pour point fixe ✓n. Or, on montre qu’on peut calculer ce point fixe par l’application répétée de f à son résultat : f(n), f(f(n)), f(f(f(n))), … On a là un moyen d’approcher ✓n d’aussi près que voulu au prix d’un calcul assez simple.
Le mot limite évoque aussi bien ce sur quoi on bute que ce vers quoi on tend. L’informatique a bien sûr des limites au premier sens, par exemple les résultats d’indécidabilité ; on parlera alors plutôt de limitation. Mais ce sont les limites au second sens qui nous intéressent ici.
Lorsqu’on recherche un point fixe, la bonne façon d’appréhender la variabilité des valeurs prises par les variables du calcul est de considérer ce qu’elles ont de commun, qu’on appelle un invariant, plutôt que ce qui les distingue et qui fait la variabilité.
Enfin, l’informatique est présente dans certains systèmes extrêmement complexes comme le système boursier, dont elle est même parfois accusée d’aggraver les emballements. Une modélisation en termes de variabilité et de stabilisation permet d’étudier ces systèmes malgré leur complexité.
Nous allons examiner plus en détails ces quatre façons de donner du sens aux mots variabilité, limite et stabilité en informatique.
Variabilité, limite, stabilité dans le foisonnement des technologies
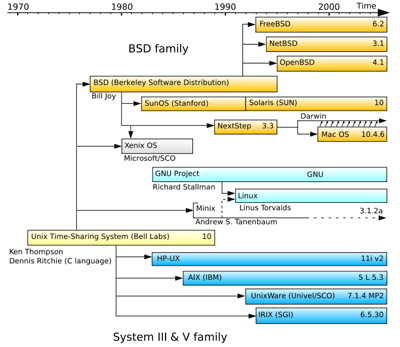
Version simplifiée de l’arbre généalogique des systèmes UNIX. Source : Wikipédia
Des documents qui retracent la généalogie de certaines technologies informatiques montrent un foisonnement que d’aucuns pourraient trouver inquiétant. Parmi les plus connus, on trouve les arbres généalogiques des systèmes UNIX, des systèmes Windows et des langages de programmation. Mais la multiplicité des versions signifie-t-elle que ces technologies ne sont pas stables ? Pas forcément. En effet, ce que ces documents ne montrent pas bien, c’est que l’histoire de ces technologies est soumise à deux forces antagonistes : la créativité qui produit de la variabilité, et le pragmatisme ou l’opportunisme qui fait que certaines branches ont beaucoup plus de succès que d’autres.
La créativité est stimulée par le besoin d’améliorer les choses, mais doit aussi prendre en compte les évolutions du reste de la technologie. C’est particulièrement frappant pour les langages de programmation. En théorie, leur expressivité formelle ne peut dépasser celle d’une machine de Turing, le modèle théorique général défini par Turing d’une machine capable d’effectuer mécaniquement tous les algorithmes possibles. Et cet objectif est atteint par presque tous les langages de programmation. Ce n’est donc pas cela que l’évolution des langages de programmation cherche à améliorer. En fait, cette expressivité est la contrepartie formelle de la fonction de commander un calculateur, donc de communiquer avec un calculateur. C’est la mission qui est le plus souvent mise en avant quand on explique la programmation, mais elle n’est pas la seule et elle est potentiellement accomplie depuis 1936 avec la machine de Turing. Cette mission a une variante technique qui est d’agir sur l’environnement du calculateur, ses capteurs, le réseau, etc. Cette variante justifie un peu la variabilité des langages de programmation, parce que la technologie évolue, mais pas tant que cela, car ce sont souvent des bibliothèques qui jouent ce rôle. Une autre mission justifie bien mieux la créativité qui règne autour des langages de programmation ; c’est celle de communiquer avec d’autres humains (voire avec soi-même) ce qu’on souhaite commander à un calculateur.
En effet, la programmation se pratique rarement seul, et demande du temps. Il faut donc être capable de produire des programmes lisibles par de nombreux partenaires, pas tous intéressés par les mêmes aspects du logiciel, et qui restent lisibles quand le temps passe. C’est là que la taille croissante des logiciels entraîne de nouvelles façons d’organiser le logiciel, par exemple la programmation par objets, et que le développement de nouveaux domaines d’application demande de nouveaux idiomes, par exemple les applications Web. Les demandes sont tellement mouvantes qu’il est illusoire d’offrir du premier coup exactement le bon langage de programmation adapté à un usage. Parfois le processus s’emballe, car les nouveaux dispositifs linguistiques sont utilisés à bien d’autres choses que ce pourquoi ils ont été développés, et cela suggère de nouveaux dispositifs. Prenons le cas d’Internet et du Web de manière générale. Ils sont constamment « poussés aux fesses » par de nouveaux usages qui commencent par détourner des protocoles existants pour aboutir à de nouveaux protocoles. On le constate avec le langage XML qui, au début, était censé faire bien ce que ne faisait pas le HTML. Et maintenant, il est utilisé comme structure de données universelle, même quand il n’y a pas d’application Web en vue.
En fait, une explication de l’extrême variabilité de ces objets informatiques, systèmes ou langages de programmation, est qu’il s’agit avant tout de logiciels, c’est-à-dire de quelque chose qu’un expert peut très facilement modifier. Le logiciel s’oppose en cela au matériel, bien plus difficile à modifier puisque cela revient à modifier une chaîne de production.
Il y a malgré tout une régulation. Certains produits ou concepts sont retenus par le public ou par l’industrie, et pas d’autres. Cela ne veut pas toujours dire qu’ils sont les meilleurs conceptuellement. Le plus souvent, cela veut plutôt dire qu’ils sont arrivés au bon moment, qu’ils présentent la bonne panoplie de dispositifs, et qu’ils sont mieux vendus par leurs promoteurs. Le cas du langage de programmation Java est typique à cet égard. Ses détracteurs lui ont reproché de ne proposer aucune innovation, et donc de « voler » le succès aux langages qui ont introduit ces innovations. Son succès s’explique sans doute par un cocktail harmonieux d’innovations proposées séparément, par l’opportunité du développement d’Internet, et par une action délibérée d’un industriel assez puissant (il s’agit bien sûr de Sun Microsystems). Ainsi, depuis 1995, Java évolue rapidement en prenant en compte l’évolution de l’environnement, des applications et des façons de développer du logiciel.
La régulation restreint le foisonnement en causant l’extinction de certaines lignées, mais on ne peut pas parler de limite vers laquelle convergerait l’évolution. On peut néanmoins parler de stabilisation si on s’en tient aux concepts. Il s’invente peu de concepts vraiment nouveaux, et l’innovation porte surtout sur la façon de les exploiter. Une alternative aux arbres généalogiques présentés plus haut serait donc l’histoire des concepts. Par exemple, la récursivité dans les langages de programmation ou le temps partagé dans les systèmes d’exploitation sont des concepts vraiment stables. C’est autour d’eux qu’il vaudrait mieux organiser les filiations d’objets informatiques. On verrait alors des changements de paradigmes liés à l’adoption de ces concepts dans différents contextes se distinguer des variations liées à l’amélioration continue des logiciels.
C’est une forme de définition où le concept défini l’est par rapport à lui-même. Bien sûr, des conditions sont nécessaires pour qu’une telle définition définisse vraiment quelque chose, mais cette façon de faire est constamment utilisée en informatique. En particulier, la plupart des langages de programmation modernes permettent de définir récursivement des procédures. D’un point de vue opérationnel, la récursivité est intimement liée à l’itération.
Voici un exemple où la même définition est présentée de manière récursive puis de manière itérative.
factorielle(n) = 1 si n vaut 1
ou n × factorielle(n-1) sinon
Cette définition récursive correspond à la définition itérative suivante :
factorielle(n) = affecter 1 à f
puis répéter
affecter n × f à f
puis affecter n-1 à n
tant que n > 1
puis retourner f comme résultat
Pour conclure sur cet aspect des choses ;
- de la variabilité beaucoup, immensément, à la folie,
- des limites point du tout (en tout cas point du tout qui concernent la variabilité observée),
- et de la stabilité un peu, par sélection naturelle.
Variabilité, limite, stabilité comme méthode de calcul
On conçoit souvent un algorithme comme l’énoncé d’opérations élémentaires et d’une façon de les ordonner. Par exemple, l’algorithme d’addition que nous avons tous appris à l’école s’énonce en termes d’opérations élémentaires fournies par une table d’addition et d’une façon de les ordonner sur le papier et dans la tête. Cet algorithme réalise la fonction mathématique de l’addition des entiers, et beaucoup de fonctions mathématiques sont susceptibles d’être « algorithmisées » de cette façon. Pourtant, pour certaines fonctions mathématiques, cette façon de faire n’aboutit pas à des algorithmes efficaces, et il vaut mieux procéder d’une tout autre façon qui consiste à poser une solution approchée, et à l’améliorer répétitivement. Les mathématiciens ont tendance à parler de méthodes itératives pour décrire cette façon de faire, même si pour l’informaticien est itératif tout ce qui itère des opérations, et par exemple, l’algorithme d’addition est certainement itératif.
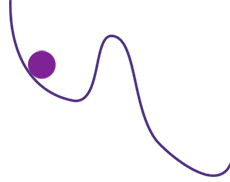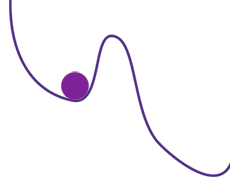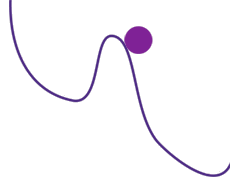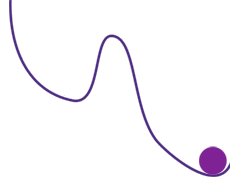
Recherche du minimum en suivant la pente du graphe. La bille tombe d’abord dans un minimum local, et doit remonter avant de pouvoir atteindre le minimum absolu.
Prenons le cas de la recherche du minimum d’une fonction, ce qui sert notamment pour la génération de trajectoires. Un algorithme, voisin de celui de Newton utilisé pour trouver les valeurs où une fonction s’annule, permet de s’approcher autant qu’on veut d’un minimum en suivant la pente du graphe de la fonction. Mais le minimum trouvé dépend de la première solution approchée, la valeur initiale, et de la façon de suivre la pente. En particulier, il peut s’agir d’un minimum local, et pas du tout du minimum absolu de la fonction. Ici, la variabilité est engendrée par la valeur initiale et la loi de progression. Pour éviter le piège du minimum local, on peut augmenter artificiellement la variabilité en imposant de temps en temps un écart arbitraire à la valeur approchée courante. On espère ainsi sortir d’un minimum local pour atteindre éventuellement le minimum absolu, ou tout au moins un minimum qui lui est proche.
Plusieurs familles d’algorithmes se réclament de cette façon de faire : par exemple, recuit simulé, utilisé notamment en traitement d’images, et méthode tabou.
La variabilité vient de la valeur initiale, de la loi de progression et des perturbations imposées aux solutions. La limite est l’objet mathématique recherché, ici le minimum d’une fonction. La limite est parfaitement définie, mais c’est le moyen de la calculer exactement qui manque. Enfin, la stabilisation peut se faire sur différents critères. Par exemple, on peut se donner un crédit de temps, et retenir la meilleure solution trouvée dans ce délai. On peut parfois estimer l’écart de la valeur trouvée à la valeur recherchée, et itérer le procédé tant que cet écart est jugé trop grand. On peut aussi constater que de nouvelles itérations n’apportent pas d’amélioration notable. Dans tous les cas, on organise la stabilisation en s’imposant un critère d’arrêt. Ce sont donc des critères heuristiques ; on regarde ce qu’on trouve, et on se demande si cela vaut la peine de continuer. Comme pour la cueillette des champignons.

Le problème du voyageur de commerce : un exemple avec 12 villes.
Prenons maintenant le cas du problème dit « du voyageur de commerce ». Étant données une liste de villes et les distances qui les séparent, il s’agit de trouver un itinéraire qui passe par toutes les villes, revient à son point de départ, et est le plus court possible (en distances cumulées). Ce problème fait partie d’une famille de problèmes pour lesquels on ne connaît pas de solution algorithmique qui soit efficace et qui calcule la réponse exacte. Par contre, si on tolère de ne pas calculer le plus court des itinéraires, mais juste un itinéraire parmi les plus courts, un algorithme itératif, au sens des mathématiciens, trouve assez facilement une solution acceptable. L’un d’entre eux donne un sens particulier au mot variabilité, puisqu’il ne part pas d’une solution approchée initiale, mais d’une population de solutions approchées telle qu’on pourrait en obtenir en choisissant l’itinéraire au hasard plusieurs fois de suite. Chaque itération consiste à évaluer les solutions approchées (par exemple, calculer la longueur de l’itinéraire), puis à ne retenir que les meilleures pour former de nouvelles solutions par combinaison de morceaux des meilleures solutions déjà calculées. L’algorithme s’arrête au bout d’un nombre fixé d’itérations ou quand l’utilisateur se déclare satisfait du résultat.
Cette façon de faire s’appelle un algorithme génétique, car elle est fondée sur la métaphore de la sélection naturelle et du partage des gènes lors de la reproduction. Ici, la variabilité réside dans les populations de solutions approchées. L’algorithme tend vers une limite formelle qui est l’itinéraire optimal, mais il n’y a pas d’opération dont on puisse vraiment assurer qu’elle améliore la solution. À l’opposé, dans le cas de la recherche du minimum d’une fonction, on sait qu’en suivant la pente du graphe de la fonction on se dirige vers un minimum. Il n’y a rien de tel ici ; on produit de nouvelles solutions d’une façon qui n’est pas du tout dirigée, et on retient les meilleures a posteriori. On constate empiriquement que cette façon de faire produit de bons résultats. Cette méthode s’applique avec succès à un grand nombre de problèmes d’optimisation. Par exemple, le calcul d’un emploi du temps pourra être confié à ce genre d’algorithme. Comme pour la recherche d’un minimum, on organise la stabilisation autour de critères heuristiques.
Pour conclure ici ;
- de la variabilité beaucoup, et elle est organisée par le programmeur (alors que personne n’organise la variabilité des logiciels),
- des limites toujours, car ces problèmes ont toujours une solution bien définie vers laquelle tendre, même si le moyen de l’atteindre n’est pas bien défini,
- de la stabilisation toujours aussi, car il faut bien arrêter ces algorithmes, mais elle s’appuie sur des critères heuristiques.
Variabilité, limite, stabilité pour parler du calcul
Le foisonnement des logiciels et l’exploration heuristique du foisonnement des solutions approchées ont ceci en commun d’être subis. En effet, les logiciels foisonnent parce que l’inventivité des hommes est sans limite, les solutions approchées foisonnent parce qu’on ne sait pas calculer directement une solution exacte. Cette troisième partie est consacrée à un aspect où en principe tout est contrôlé par le programmeur, et pourtant variabilité, limite et stabilité fournissent une métaphore intéressante.
Prenons le cas d’un programme de tri. Il résout un problème bien défini par une méthode directe, qui trie effectivement un ensemble de valeurs. Il n’est pas si simple de se convaincre que le programme réalise correctement un tri dans tous les cas de figure. Il y a des variables, des tests et des itérations. Les valeurs prises à un moment donné par les variables constituent l’état courant du programme. Chaque pas d’une itération calcule un nouvel état courant, et pour peu qu’il y ait de nombreux pas d’itération, il y aura de nombreux états courants. S’il est bien fait, le programme s’arrêtera dans un état où toutes les valeurs sont bien triées. On ne peut pas se convaincre que le programme est correct en énumérant les états, car ceux-ci dépendent des données initiales. Trier {3,1,2} ne produit pas les mêmes états que trier {9,1,8,2,7,3,6,4,5}. Le programmeur se trouve dans la situation inconfortable où le programme qu’il a écrit lui-même, qui est fini et même relativement petit, engendre un ensemble potentiellement infini de situations, les états. Un texte fini parfaitement maîtrisé engendre donc un ensemble infini d’états, pas du tout maîtrisable directement. À première vue, le programmeur ne perçoit que la variabilité des états, tous singuliers.
La bonne façon de maîtriser cette variabilité est d’en prendre le contre-pied et de considérer ce qui est constant. Ce ne sont pas les valeurs des variables qui peuvent être constantes, puisque la raison d’être des variables est justement de changer de valeur. Par contre, les valeurs des variables peuvent entretenir des rapports ou des relations constantes. On appelle cela un invariant.
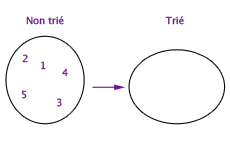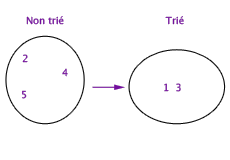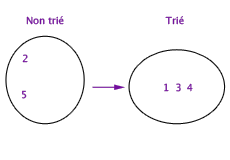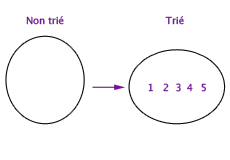
Exemple de tri de 5 éléments de l’ensemble non trié vers l’ensemble trié.
Par exemple, l’invariant d’un programme de tri peut être qu’il entretient deux ensembles de valeurs, tels que l’union de ces ensembles est toujours égale à l’ensemble de valeurs initiales, un des ensembles est trié, l’autre ne l’est pas. Voilà un invariant. Ce qui change quand on change d’état est le contenu effectif des deux ensembles, mais l’invariant doit rester. Initialement, l’ensemble trié est vide et l’ensemble non-trié est celui des valeurs initiales. Puis chaque itération consiste à prendre un élément dans l’ensemble non-trié et à le ranger en bonne place dans l’ensemble trié. Si chaque étape d’itération contribue effectivement à conserver cet invariant, le programme est certain de produire un état où l’ensemble trié contient toutes les valeurs initiales convenablement rangées, et l’ensemble non-trié est vide. On a donc dépassé la variabilité des états en lui opposant l’invariabilité de certaines propriétés plus abstraites. Ce faisant, un état limite et la stabilisation du programme s’imposent à l’esprit.
Pour conclure temporairement ;
- de la variabilité oui, à la folie, à l’infini (infini potentiel, comme il se doit), dans les différents états que peut atteindre un programme,
- des limites et de la stabilité, oui, en considérant les invariants plutôt que la variabilité brute.
Il y a même un invariant méthodologique ; il vaut toujours mieux décrire un système informatique en commençant par ses invariants qu’en commençant par le détail de ses aventures.
On vient de voir que la situation du programmeur peut vite devenir inextricable s’il ne s’impose pas un minimum de méthode. Considérons maintenant la situation du concepteur d’un langage de programmation, un de ceux qui alimentent la variabilité des programmes informatiques. Là où le programmeur doit s’assurer que dans tous les cas son programme est correct, le concepteur d’un langage de programmation doit décrire dans tous les cas (tous les programmes) ce que fait dans tous les cas (tous les états) un programme écrit dans son langage. Il se situe à un étage d’abstraction au-dessus. Une approche assez abstraite — mais fructueuse — est de considérer qu’un programme recherche un point fixe d’une fonction, et c’est le travail du concepteur du langage de programmation de spécifier quelle fonction est associée à quel programme. Si la fonction n’a pas de point fixe, le programme bouclera ; si elle en a un, la mise en œuvre du langage de programmation doit faire qu’on le trouve. On substitue donc à la variabilité des calculs qu’il est possible d’exprimer dans un langage de programmation, un principe unique de recherche de point fixe, donc de limite.
Pour conclure ;
- de la variabilité oui, à la folie, qui combine la variabilité des programmes et celle des états de calcul,
- des limites oui, en en faisant le principe même du calcul (rechercher une limite),
- de la stabilisation oui, mais…
… depuis 1936, nous savons que tout langage de programmation qui permet d’exprimer toutes les fonctions totales (définies partout) permet aussi d’exprimer des fonctions qui ne le sont pas, et qu’il n’y a pas moyen d’écrire un programme capable de décider si un programme donné décrit une fonction totale ou non. C’est le fameux problème de l’arrêt. La stabilité, ou plutôt le manque de stabilité, demeure donc le talon d’Achille du programmeur.
Nous venons d’exposer comment donner du sens aux mots variabilité, limite et stabilité en informatique du point de vue interne de l’informatique. Quel que soit le niveau d’analyse, que l’on considère les technologies, la programmation, ou encore la théorie de la calculabilité, la variabilité est un moteur de l’informatique. Dans un autre contexte on parlerait de complexité ; l’informatique est souvent utilisée pour gérer la complexité, mais elle en engendre aussi. La question des limites et de la stabilité est plus subtile et dépend du contexte. Au niveau technologique, il n’y a pas de limite, et la stabilisation n’est jamais totale ; l’informatique est une activité humaine. On peut dire que c’est une langue vivante. Au niveau de la programmation, les limites sont fixées par les spécifications, et la stabilisation peut se décréter, en se contentant parfois de solutions approchées. En théorie de la calculabilité, la limite, ou plutôt la recherche de celle-ci, devient le moteur du calcul, mais la stabilité ne se décrète pas. Elle échappe même au calcul, puisque c’est une propriété indécidable.
Tous ces points de vue sont internes à l’informatique et finalement assez simples, car ils concernent des systèmes artificiels sans leurs interactions avec le monde réel. Or, le monde réel recèle lui aussi de la variabilité et des phénomènes de stabilisation vers des comportements émergents, qui peuvent être étudiés par le biais de la modélisation.
Variabilité, limite, stabilité comme méthode de modélisation
Pas facile d’étudier variabilité, limite et stabilité pour des systèmes complexes, dynamiques et non linéaires. Pourtant, dans les années 1960, a débuté une nouvelle manière d’envisager l’étude des systèmes physiques, basée sur des modèles mathématiques de la théorie des systèmes dynamiques non linéaires. La théorie des catastrophes de Thom, la théorie des états critiques ou la théorie du chaos, par exemple avec Gleick en 1991, en sont des étapes importantes. Cette théorie permet d’aborder des phénomènes qui mettent en évidence des comportements non réguliers, apériodiques et complexes.
L’idée la plus fascinante est celle de l’émergence de « comportements », à partir des propriétés internes et externes du système, sous l’influence des contraintes qui le constituent ou qui pèsent sur lui, sans aucune « programmation » ou « planification préalable ». Le comportement émerge sans nécessité de planification, de programmation par des instances extérieures au système.
Pour formaliser cette idée, on parle d’« attracteur ». Plusieurs types d’attracteurs sont définis : les points fixes correspondent à un état vers lequel semble converger le système ; on peut citer l’exemple du pendule, qui tend sous l’action de la pesanteur à rejoindre sa position de repos, mais aussi celui du résultat vers lequel converge un calcul. Les cycles limites renvoient à la répétition d’une trajectoire. On retrouve ce type d’attracteur dans les oscillateurs auto-entretenus mais aussi dans le comportement d’un calcul qui boucle. Enfin, les attracteurs étranges ou chaotiques – comme l’attracteur de Lorenz – présentent une trajectoire plus complexe, qui bien que ne se répétant jamais à l’identique, conserve une part de déterminisme.
Cette complexité est liée à la présence de nombreux éléments hétérogènes en interaction. Le concept de degrés de liberté est central dans cette approche de la complexité. On peut concevoir les degrés de libertés comme les paramètres libres d’un système, c’est-à-dire susceptibles de varier indépendamment des autres.
Au-delà, on appelle bifurcation ou transition de phase, une modification qualitative du comportement du système. Une bifurcation résulte d’une modification du paysage des attracteurs. Les bifurcations constituent une événement majeur de la dynamique des systèmes complexes : ils correspondent au changement de comportement, c’est-à-dire à la disparition ou à l’apparition d’attracteurs.
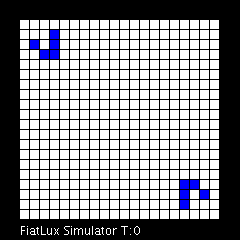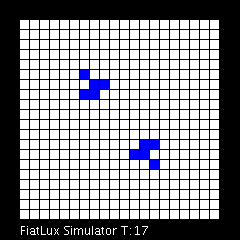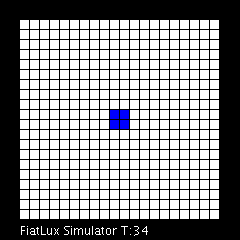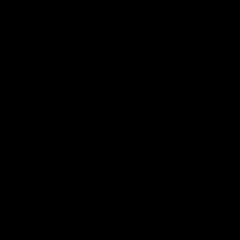
Dans le modèle dit du Jeu de la vie, qui met en évidence le comportement d’automates cellulaires, l’apparition des glisseurs est un phénomène qui illustre la propriété d’émergence. Animation produite avec le logiciel FiatLux © Nazim Fatès
En informatique, elle est reliée au concept d’émergence que l’on caricature souvent par la maxime « le tout est plus que la somme des parties ». Le système acquiert de ce comportement collectif des caractéristiques nouvelles non réductibles à la superposition du comportement des unités le constituant. A contrario, il n’hérite pas nécessairement toutes les propriétés de ces unités (des approximations, moyennes sur un ensemble d’unités, leur font perdre la structure que l’on pouvait avoir au niveau d’une unité).
Les automates cellulaires et l’intelligence en essaim illustrent très bien ce concept d’émergence. Les réseaux de neurones artificiels en sont le plus bel exemple informatique : programmés à partir de règles simples, ils peuvent offrir une approximation de mécanismes de forte complexité.
Cette description des systèmes dynamiques s’applique à de multiples domaines, des neurones du cerveau au changement climatique, en passant par les nouveaux moyens de traiter les déchets chimiques, et même l’enseignement…
Lorsqu’on enseigne les sciences, il se produit un changement de conceptions chez l’élève. Dans la dynamique non linéaire, les changements correspondent à des bifurcations. On peut chercher à montrer, en utilisant la théorie des systèmes dynamiques complexes, que l’acquisition des concepts scientifiques comporte des changements successifs de conceptions intermédiaires entre le sens commun et le savoir scientifique : des ruptures épistémologiques. Il y a simultanément stabilité (dans le comportement global de l’apprenant) et variabilité (dans l’adéquation à chaque situation particulière).
Relisez cet article et peut-être que dans votre esprit de nouveaux attracteurs surgiront : une bifurcation sur le chemin de la connaissance.
Nos remerciements à Thierry Viéville pour sa contribution à la partie de ce document portant sur la modélisation.
Newsletter
Le responsable de ce traitement est Inria. En saisissant votre adresse mail, vous consentez à recevoir chaque mois une sélection d'articles et à ce que vos données soient collectées et stockées comme décrit dans notre politique de confidentialité
Niveau de lecture
Aidez-nous à évaluer le niveau de lecture de ce document.
Votre choix a été pris en compte. Merci d'avoir estimé le niveau de ce document !

Olivier Ridoux
Professeur d'informatique à l'Université de Rennes, chercheur à l'IRISA.