Ces surfaces qui nous entourent

Au premier abord, la notion de surface nous est familière. Il n’est pas nécessaire de cogiter bien longtemps pour voir poindre dans notre esprit plusieurs sens à ce mot. Sans doute surgira d’abord l’acception « surface d’un objet » qui représente son enveloppe extérieure et en particulier, son apparence. En faisant appel à nos souvenirs de mathématiques, nous nous remémorerons comment définir et surtout comment calculer la surface – c’est-à-dire ici la superficie – d’une figure géométrique. Sans parler de la physique où l’on considère les surfaces de contact délimitant deux milieux différents pour y étudier des phénomènes parfois complexes (diffusion et réfraction de la lumière, interactions entre les fluides, etc.).

Comment traiter la notion de surface dans le contexte de la science informatique ? Le point de départ que nous avons choisi pour cette évocation est l’image, au sens numérique du terme.

Surfaces et modélisation

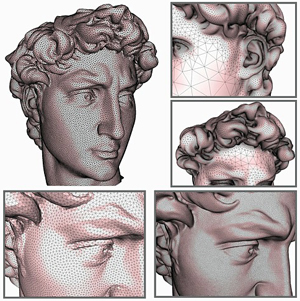
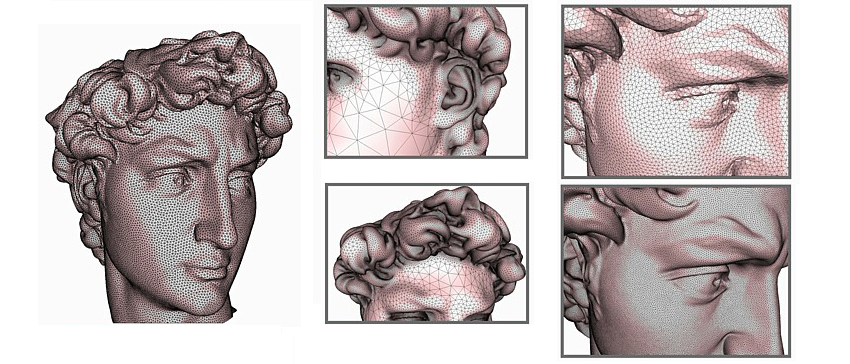
Échantillonnage et maillage de surfaces.
© INRIA / GEOMETRICA

Une image numérique de synthèse est le résultat de calculs exploitant une description — également appelée modèle — de l’objet que l’on veut visualiser. Ce modèle décrit la forme de l’objet mais aussi son apparence. La façon la plus courante de qualifier cette forme est de décrire son enveloppe extérieure : on parle de modélisation surfacique. Pour définir la forme d’un objet simple, comme un cube, on peut par exemple donner la liste des coordonnées de ses sommets. Ces sommets sont ensuite projetés sur l’espace de visualisation (l’écran), puis les pixels des faces ainsi projetées sont affichés avec la couleur de l’objet. Malheureusement pour la simplicité des calculs mais heureusement pour la diversité, la nature n’est pas faite que de surfaces planes. Les mathématiciens et les informaticiens ont donc dû ensemble mettre au point des méthodes de modélisation plus complexes prenant en compte les surfaces courbes.

La première notion importante est celle de maillage : on fait une approximation « au mieux » de la surface extérieure par un ensemble de polygones adjacents en leurs sommets appelés mailles. Arrêtons-nous quelques instants sur la notion de « meilleure » approximation.

Pour obtenir une image de synthèse réaliste d’un objet quelconque, il est nécessaire de reproduire l’influence de plusieurs sources lumineuses sur cet objet ainsi que les interactions entre la lumière et la matière qui se déroulent sur sa surface extérieure. Bui Tuong Phong mit au point dès 1973 un modèle de calcul d’éclairement encore très utilisé aujourd’hui pour simuler cet éclairement, l’ombrage de Phong. Pour des raisons d’efficacité — et plus précisément de temps de traitement —, il est difficile de faire ce calcul d’éclairement en tous les points de la surface de l’objet ; on le réserve donc uniquement aux sommets du maillage. Les résultats ainsi obtenus sont utilisés pour calculer la couleur des points par interpolation, par exemple avec l’algorithme mis au point en 1971 par Henri Gouraud.

On voit alors apparaître un antagonisme très classique en informatique : pour obtenir un meilleur réalisme dans l’image, on a intérêt à utiliser un maillage le plus précis possible afin de coller au plus près à la forme réelle de l’objet et de tous ses détails. Mais pour avoir un maillage précis, on a besoin d’un grand nombre de sommets, ce qui implique un nombre important de calculs et donc un temps de synthèse parfois rédhibitoire. Alors, comment fait-on pour affronter ce dilemme ? On utilise des modèles de surfaces multi-résolutions. Ceux-ci proposent plusieurs niveaux de détails : un niveau grossier qui engendre une qualité médiocre mais un temps de calcul très rapide (par exemple, pour visualiser des objets lointains, à l’arrière-plan d’une scène) et un niveau précis qui fournit une bonne précision au détriment d’une durée de calcul plus importante (par exemple, pour les objets situés au premier plan). On parle alors de surface de subdivision, où la précision dépend du niveau de détail souhaité par l’utilisateur. À cette occasion, on peut évoquer la notion de surface fractale, inventée par des géographes pour représenter la surface des côtes en fonction de l’échelle de leurs cartes : elle permet de représenter une courbe ou une surface à différents niveaux de précision.

Un modèle de surface implicite.
© INRIA / EVASION

Mais il reste des surfaces trop complexes, pour être correctement représentées de cette façon. Les mathématiciens ont développé des théories de représentation de surface par interpolation. Issues des courbes et étendues aux surfaces, ces théories sont regroupées dans la grande famille des Splines. Citons les courbes de Bézier inventées en 1962 par l’ingénieur français Pierre Bézier pour concevoir des voitures chez Renault. Un autre exemple en sont les courbes NURBS, très populaires parce qu’elles ont un format de stockage normalisé donc qui autorise les échanges entre les logiciels de CAO.

On peut aussi citer les surfaces implicites décrites par tous les points satisfaisant une équation du type f (x, y, z) = 0. Représenter de telles surfaces permet de visualiser des surfaces équipotentielles. En fusionnant plusieurs de ces surfaces élémentaires, on peut représenter des formes élastiques, des fluides, et surtout à les animer, ce qui explique leur grand succès parmi les infographistes. En effet, elles ont permis de lever certaines limitations des autres modèles pour décrire des objets de forme douce ou construits en accolant des formes élémentaires comme par exemple une main formée d’une paume et de cinq doigts, ce qui avec les approches précédentes entraîne des problèmes de raccordement géométrique de surfaces.

Surfaces et imagerie

Pour créer des modèles de surfaces complexes, il existe deux grandes méthodes : l’acquisition de la géométrie d’objets réels et la modélisation à l’aide d’outils logiciels interactifs appelés modeleurs.

L’acquisition de la géométrie d’objets réels fait appel à des capteurs comme des scanners 3D qui, en mesurant les temps de vol de rayons lasers, produisent une liste de coordonnées de points situés sur la surface de l’objet. On reconstruit alors une surface à partir de ce nuage de points, par exemple en utilisant des théories comme la triangulation de Delaunay ou le diagramme de Voronoï. Récemment, les chercheurs ont mis au point des techniques d’acquisition basées sur l’analyse de flux vidéos issus de caméras filmant un ou plusieurs objets en mouvement. Ces solutions se rapprochent des techniques de capture de mouvement très utilisées par exemple pour fabriquer des jeux vidéo qui reproduisent les gestes de sportifs de haut niveau.

Le monde médical peut également s’inscrire dans cette première famille : dans ce domaine, on utilise des capteurs comme les IRM ou les scanners qui produisent des images parallèles équidistantes (procédé de tomographie) afin de mieux analyser une partie du corps du patient, d’abord pour comprendre la pathologie dont il souffre, ensuite pour planifier si besoin un geste chirurgical.

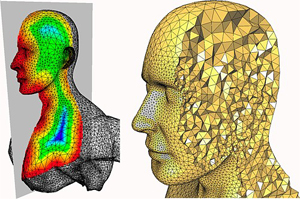
Maillage volumique pour la simulation.
© INRIA / GEOMETRICA

La modélisation à l’aide d’outils logiciels interactifs requiert quant à elle l’utilisation de modeleurs comme Blender, 3DS ou encore Catia. Inventés par et pour les ingénieurs travaillant en Conception Assistée par Ordinateur (CAO), puis développés par les concepteurs d’images de synthèse et adoptés par les infographistes (par exemple, dans les studios de jeux), les modeleurs ont progressivement migré du monde professionnel vers le grand public. Ils permettent par exemple de générer des surfaces de révolution créées par la rotation d’une courbe (également appelée profil) autour d’un axe ou encore des surfaces d’extrusion créées par la translation d’un profil suivant un axe (utilisées par exemple en architecture). Ces modeleurs sont aujourd’hui un des vecteurs importants de la diffusion de la notion de surface au sens informatique.

Évidemment, tous ces modèles de surface ne servent pas seulement à calculer des images. Beaucoup d’autres utilisations sont souvent regroupées sous la notion de simulation numérique. Il s’agit, à partir de la description des caractéristiques géométriques et physiques d’un objet, de prédire son comportement à l’aide de calculs. Que ce soit pour déterminer l’aérodynamisme d’un avion, vérifier le comportement d’une voiture face aux chocs ou encore tester la résistance d’un pont au passage des véhicules, les modèles de surface sont toujours au cœur des calculs de simulation.

Surfaces et réalité virtuelle

Équipement pour système virtuel : lunettes et capteurs.
© INRIA / Photo C. Lebedinsky

Une « nouvelle » utilisation de la notion de surface en sciences du numérique est la réalité virtuelle, qui permet de reproduire des phénomènes complexes en intégrant dans le processus simulé un ou plusieurs opérateur(s) humain(s) interagissant par l’intermédiaire d’interfaces (matérielles et logicielles) avec un monde virtuel. Technologie souvent assimilée à de la science-fiction ou à un gadget à ses débuts, elle est maintenant partie intégrante de l’activité d’un nombre croissant d’entreprises et de laboratoires pour concevoir, comprendre, expliquer, apprendre… Si nous retrouvons encore des images de synthèse pour visualiser les mondes virtuels dans lesquels évoluent les utilisateurs, il existe bien d’autres exploitations des surfaces en réalité virtuelle.

Pour ne pas faire comme Bourvil qui traverse à sa guise les murs dans le film « Le passe-muraille », il est indispensable dans un monde virtuel de détecter les collisions entre les entités en mouvement. Là encore, c’est la surface extérieure des objets qui est utilisée pour réaliser des tests d’intersection.

Pour mieux immerger l’utilisateur, c’est-à-dire mieux « tromper » son cerveau, on doit optimiser la quantité et la qualité des informations sensorielles qu’il reçoit du monde virtuel. Le premier sens visé est la vue, puis l’ouïe grâce à une simulation sonore, et enfin le sens du toucher. Pour simuler les sensations ressenties par exemple lors de la préhension d’un objet, les chercheurs ont développé des méthodes dites haptiques utilisant des matériels qui reproduisent les forces s’exerçant sur la surface de la peau. On parle de retour d’effort, un concept connu depuis plusieurs années par les férus de jeux vidéo. Mais il est également possible de simuler ces sensations tactiles sans matériel actif.

Surfaces et interaction homme-machine

Écran Multi touch multi-utilisateurs.
© INRIA / Photo Kaksonen

Un autre domaine informatique où la notion de surface est fondamentale est celui de l’interaction entre l’humain et la machine (IHM), qui régit les façons d’utiliser une application informatique. Popularisées très récemment par la sortie de l’iPhone qui leur doit en partie son succès, les interactions tactiles ont été inventées en 1972 à l’université d’Illinois. Elles reposent sur un principe simple : on utilise son doigt pour pointer et sélectionner des zones de l’écran qui sont associées à des choix ou à des fonctions. Par exemple, répondre à une question, saisir des lettres formant un texte ou encore redimensionner une photo en éloignant deux de ses extrémités.

Le grand public a massivement plébiscité ces principes avec l’iPhone. Une des raisons de cette adhésion en est leur simplicité d’utilisation : aucun périphérique n’est nécessaire ; ni souris ni clavier. Un autre des principes de base de ces interfaces tactiles est la juxtaposition des surfaces de visualisation et d’interaction. Contrairement aux ordinateurs classiques où la première se déroule sur un écran et la seconde sur le bureau via une souris par exemple (voir 50 ans d’interaction homme-machine : retours vers le futur). Microsoft a parfaitement identifié cette importance en baptisant « Surface » son produit d’interaction vedette qui préfigure nos futurs ordinateurs qui seront tous dotés de surfaces tactiles et capable de les gérer. Une autre direction de recherche est la mise au point de techniques d’interaction tactiles 3D augmentant les fonctionnalités des interfaces aujourd’hui restreintes à des interfaces 2D.

Les surfaces ont déjà une longue histoire dans le domaine des sciences du numérique. Et les choses n’étant jamais figées dans ce secteur, il reste encore beaucoup à inventer…