La brouette de Monge ou le transport optimal
Ce problème, popularisé sous le nom de « Brouette de Monge » est donc le premier exemple historique de recherche opérationnelle.
Cette question a été réexaminée dans les années 1940 par Leonid Kantorovich (un des quelques mathématiciens lauréats du prix Nobel d’économie) à propos d’allocation optimale des ressources. Dans son œuvre, il cherche à résoudre ce problème : pour la production de quels biens et services les rares facteurs de production (travail, capital, etc.) doivent-ils être mis en œuvre afin de réaliser une satisfaction maximale des besoins ?
Bien d’autres questions (files d’attente, gestion de stock, classement, etc.), que nous ne détaillerons pas ici, font partie de ce domaine. Il s’agit toujours de trouver comment passer de la situation initiale à la configuration finale de la meilleure manière possible, c’est-à-dire par le meilleur chemin dans l’espace compliqué qui correspond à l’application considérée.
Une notion de géodésique pour un nuage de points ?
Le point clé de la théorie est le suivant : dans un espace compliqué, il existe des méthodes efficaces pour trouver le meilleur chemin (qui n’est pas forcément la ligne droite). Un tel chemin optimal s’appelle une géodésique.
Le concept géométrique de géodésique est bien adapté à la description d’un « point mobile », ou, pour prendre une image plus physique, d’une « particule ponctuelle », astreinte à se déplacer au moindre coût d’un point à un autre sur une surface donnée. Pensons à la trajectoire d’un vol transatlantique, modélisée par le mouvement d’un point à la surface du globe terrestre.
Ce qui est vrai pour un point peut être vrai pour un « nuage de points » ou d’autres objets : les manipuler au mieux revient à trouver le meilleur chemin possible, pour amener ces objets tous ensemble de leur état initial à l’état final désiré. C’est sur cette idée si simple et si riche que s’est bâtie la brouette de Monge que nous allons empoigner.
Transport d’un nuage constitué d’un nombre fini de points
Pour une vision concrète du problème, il est bon de considérer le cas d’un nuage fini constitué par exemple de quatre points. Pour simplifier, on se place dans le plan (où les géodésiques sont les droites), plutôt que dans l’espace à trois dimensions.
On se donne la configuration du nuage à deux instants donnés, et on cherche comment le transporter de façon optimale entre les deux configurations. À l’instant de départ, le nuage est donc défini par une liste de quatre points dans le plan A1, A2, A3, A4, et à l’instant final par quatre autres points B1, B2, B3, B4.
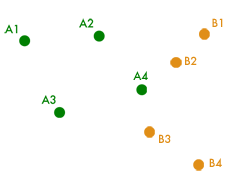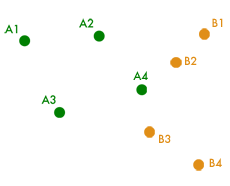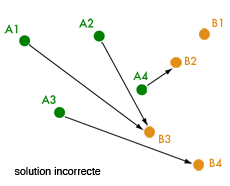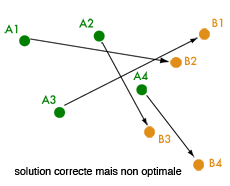
Transport de quatre points.
Un point clé à comprendre est qu’on ne se soucie aucunement de l’individualité des « particules » et que leur numérotation est arbitraire. Ainsi, il est parfaitement possible de transporter, par exemple, A1 vers B3, A2 vers B1, A3 vers B4 et A4 vers B2. (En revanche, on n’est pas autorisé à déplacer A1 et A2 vers B3 en laissant B4 vacant, par exemple.)
Il faudra donc chercher une solution optimale parmi tous les arrangements possibles, c’est-à-dire parmi toutes les bijections des indices {1, 2, 3, 4} vers eux-mêmes. Le nombre d’arrangements possibles des N premiers entiers s’appelle la factorielle de N. Il vaut 24 pour N = 4 (et… 21794572800, soit plus de 20 milliards, pour N = 15).
La bijection σ correspondant à notre exemple s’écrit :
σ(1) = 3, σ(2) = 1, σ(3) = 4, σ(4) = 2.
Trouver la solution optimale revient à minimiser un coût, que l’on choisira ici comme la somme des distances entre les points de départ et les points d’arrivée, portées à une certaine puissance p, par exemple p = 1 ou p = 2, que l’on fixe une fois pour toutes.
Notez que la puissance p ne joue aucun rôle si le nuage se réduit à un seul point, c’est-à dire si N = 1, ce qui nous ramène alors au cas des géodésiques habituelles. En revanche, dans le cas général, deux exposants p différents peuvent conduire à des solutions optimales différentes.
Le problème traité par Monge correspondait au cas p = 1 (où le coût est la somme des distances parcourues). Dans la suite, on regardera le cas p = 2 (le coût est donné par la somme des carrés des distances), qui offre des applications intéressantes. Il convient de noter que certaines applications à l’économie requièrent d’autres valeurs de p (en particulier des valeurs fractionnaires situées entre 0 et 1 pour certains modèles), mais les principes utilisés restent similaires.
Dans tous les cas, comme p est fixé, le problème se réduit à trouver la bijection des indices qui rend ce coût minimal.
Un problème d’optimisation combinatoire
Ainsi formulé, notre problème de transport optimal appartient à une branche importante des mathématiques, l’optimisation combinatoire. Dans cette discipline, notre problème est considéré comme « facile ». En effet, il existe des algorithmes qui permettent de trouver l’arrangement optimal en un nombre d’opérations arithmétiques proportionnel au cube du nombre de points. (Cela veut dire que, sur un ordinateur où les opérations s’effectuent séquentiellement, sans parallélisme, le temps de calcul pour N points divisé par N3 restera borné quelle que soit la taille de N, aussi bien pour N = 4 que pour N = 1 000 000. Ce calcul pourra donc toujours être effectué.)
Rappelons que le nombre d’arrangements possibles est la factorielle de N, et qu’il est donc déjà remarquable de rendre le temps de calcul cubique par rapport à N. (En effet, si pour N = 4 la factorielle vaut 24 et reste modérée, lorsque N est grand, elle augmente grosso modo comme (N/e)N 1/2, où e = 2,71828…, bien plus vite que N3 en tous cas, et devient rapidement …astronomique. C’est toute la difficulté de l’optimisation combinatoire.)
Imaginons que nous souhaitions relier des points A1, A2, A3, A4 à d’autres points B1, B2, B3, B4 de façon que chaque point soit relié à un et un seul autre point, et que les chemins soient de longueur minimale.
Pour cela, nous commençons par répertorier tous les chemins possibles, avec leur longueur. Notons L11 la longueur du chemin de A1 à B1, L12 celle du chemin de A1 à B2, et ainsi de suite par exemple L34 celle du chemin de A3 à B4. Toutes ces longueurs sont regroupées dans un tableau, où chaque ligne représente toutes les longueurs issues d’un point A1, A2, A3 ou A4 et chaque colonne les longueurs aboutissant à B1, B2, B3 ou B4.
| L11 | L12 | L13 | L14 |
| L21 | L22 | L23 | L24 |
| L31 | L32 | L33 | L34 |
| L41 | L42 | L43 | L44 |
Se pose alors le problème d’affectation : comment choisir parmi les différentes possibilités ?
Nous remarquons que si toutes les longueurs issues d’un point sont raccourcies de la même quantité, par exemple si on réduit L11, L12, L13 et L14 de la même quantité, cela ne change rien au problème d’affectation, puisqu’il faudra de toutes façons choisir l’une de ces longueurs pour un chemin partant de A1. Donc si on soustrait une constante à une ligne de ce tableau, le problème reste le même.
De même, si toutes les longueurs aboutissant à un point sont raccourcies de la même quantité, c’est-à-dire si on soustrait une constante à une colonne de ce tableau, le problème reste le même.
Cela ne change certes pas le problème… mais simplifie la solution !
En effet, si pour chaque ligne et chaque colonne du tableau, nous soustrayons le plus petit élément, nous faisons apparaître des zéros. Ensuite, nous pouvons travailler sur une partie du tableau, pour réduire encore les longueurs, mais en nous assurant de conserver le même problème. Et il faudra recommencer tant que nous pouvons faire apparaître des zéros. Il faut ainsi au pire balayer environ quatre fois ce tableau de taille 4 x 4, ce qui donne une complexité cubique.
Cette « méthode hongroise » permet de faire apparaître des solutions dans lesquelles le coût de l’affectation est nul, et nous sommes sûrs d’obtenir une solution optimale.
Si notre problème a été peu étudié du point de vue de l’optimisation combinatoire théorique (contrairement au fameux problème du voyageur de commerce par exemple), en pratique, les algorithmes connus sont peu performants lorsque N devient grand (au delà du millier, disons). On peut rêver d’un algorithme dont le coût de calcul croîtrait à peu près proportionnellement à N (comme c’est le cas, à une « correction logarithmique » près, d’algorithmes fameux, comme le tri rapide de N nombres réels, la transformée de Fourier discrète rapide, etc.). Les applications en seraient spectaculaires. Mais pour approcher ce rêve, il faut changer de point de vue, et considérer non plus un nombre limité de points, mais des points en très grand nombre, voire une infinité de points.
Transport optimal d’un nuage « continu »
Comme souvent en mathématiques et en physique, la limite « continue » du problème « discret » précédemment discuté permet de mettre en jeu toute la force du calcul différentiel et intégral.
Pour faciliter l’exposé, on considère des nuages de points distribués dans l’espace euclidien à d dimensions (où d est un entier 1, 2, 3…) qui généralise notre espace physique à 3 dimensions. Pour simplifier, il est possible de se limiter au cas du plan à 2 dimensions. Rappelons que, dans ce cas, les courbes géodésiques (les « chemins les plus courts ») sont simplement les lignes droites.
Dorénavant, notre nuage de points sera décrit, respectivement au départ et à l’arrivée, par deux fonctions (deux « densités de probabilité ») donnant, en tout point x de l’espace, la densité du nuage, soit α(x) au départ et β(x) à l’arrivée. Ce sont deux nombres réels positifs ou nuls, dont l’intégrale par rapport à x vaut 1.
Dans le cas de l’exposant p = 2 et de l’espace euclidien à d dimensions, le principal résultat théorique a été obtenu dans la seconde moitié des années 1980. Il nous dit la chose suivante : connaissant les deux fonctions de densité α et β, on peut leur associer une autre fonction, notée Φ, qu’on appelle « potentiel ». Ce potentiel permet de définir la trajectoire optimale de chacune des particules constituant le nuage, de la densité α de départ vers la densité β d’arrivée.
Et là, paradoxalement, d’avoir « compliqué » le problème permet de le résoudre plus simplement.
Le potentiel et son gradient
Plus précisément, chaque particule sera transportée en ligne droite à vitesse constante, cette vitesse dépendant de la variation de l’espace à proximité du point de départ. Mathématiquement, la variation est représentée par le gradient du potentiel Φ.
Rappelons que, pour une fonction Φ donnée, le gradient de Φ peut se représenter assez facilement, au moins en dimension d = 2, en traçant les lignes de niveau de Φ, comme sur une carte d’état major où Φ(x) serait l’élévation du relief au point x. Le gradient DΦ(x) est alors un vecteur perpendiculaire à la ligne de niveau passant par x, dont la longueur est inversement proportionnelle à la distance (infinitésimale) des lignes de niveau voisines. Le gradient est donc d’autant plus fort que les lignes sont resserrées.
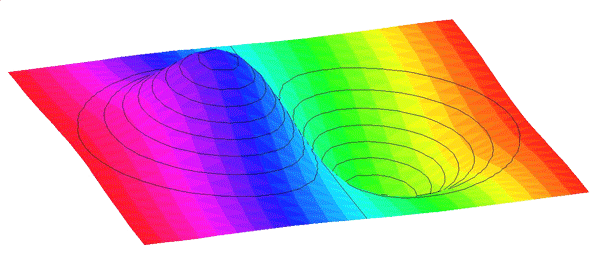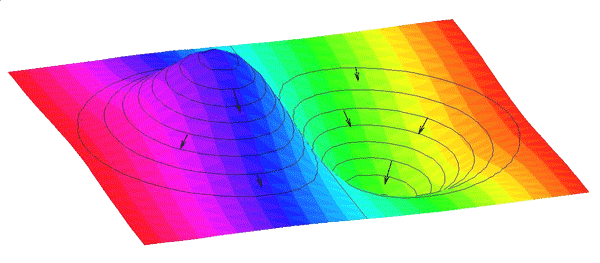
Un exemple de surface avec quelques valeurs de gradient représentées par les flèches qui sont dans le direction de la plus grande pente et dont la taille correspond à l’amplitude de cette pente.
Ainsi, le transport optimal de la particule située au départ au point x s’effectuera en ligne droite, perpendiculairement à la ligne de niveau de Φ passant par x, et la vitesse de parcours v sera d’autant plus grande que les lignes de niveau se resserrent autour de x.
Il s’avère que les vitesses des particules dans le transport optimal « dérivent » d’un potentiel précisément parce que l’on ignore l’individualité des particules constituant le nuage de points. (C’est l’équivalent, en « continu », de l’arrangement optimal précédemment discuté dans le cas « discret » d’un nombre fini de particules.)
Une propriété essentielle du potentiel est que deux particules issues de deux points différents x et y ne peuvent pas se croiser au cours de leur transport. Cette propriété est cruciale pour les applications discutées plus bas.
En un temps t intermédiaire entre le temps de départ 0 et le temps d’arrivée 1, la position de la particule partie de x sera donnée par la formule :
x + t v avec v = DΦ(x)
où l’on note v la vitesse de la particule et DΦ(x) le vecteur gradient de Φ au point x.
Pour deux points, l’égalité
x + t DΦ(x) = y + t DΦ(y)
est impossible pour t inférieur à 1 et x distinct de y. (L’égalité est acceptable pour t = 1.)
Mathématiquement, cela se traduit par la convexité de la fonction Φ(x) augmentée de la moitié de la norme euclidienne de x portée au carré.
Enfin, la théorie montre que le potentiel, ou plutôt son gradient, est uniquement déterminé par la donnée des fonctions de densité de départ et d’arrivée. Sous des hypothèses adéquates, le calcul différentiel traduit cette relation par l’équation différentielle (« aux dérivées partielles ») dite de Monge-Ampère (sans que la relation avec le problème de Monge ait été, semble-t-il, établie lors de sa dénomination).
L’équation de Monge-Ampère est bien connue des géomètres car elle permet, dans certains cas, de reconstruire une surface connaissant le produit de ses rayons de courbure (principaux) en tous points.
Cette équation s’écrit ainsi :
α(x) = β(x + DΦ(x)) det(I + D2Φ(x))
Ici, D2Φ(x) désigne la matrice carrée des dérivées partielles d’ordre 2 de Φ, I la matrice identité correspondante et det désigne le déterminant. La condition de convexité revient à dire que la matrice I + D2Φ(x) est, en tout point x, symétrique semi-définie positive.
Une application inattendue : modifier les images
Ce problème d’essence mathématique rencontre déjà des applications bien concrètes, comme le montre cet exemple récemment étudié par l’équipe de Jean-Michel Morel à l’ENS de Cachan.
On dispose de l’image numérisée d’une peinture dont les couleurs sont défraîchies. Ces couleurs sont numériquement codées selon les couleurs élémentaires bleue, rouge et verte. À chaque pixel est donc associée une certaine proportion de bleu, de rouge ou de vert. En balayant les N pixels de l’image numérique, on obtient un nuage de N points dans l’espace tridimensionnel des couleurs. (Il s’agit d’un espace abstrait, pas de notre espace physique.) Par ailleurs, on a une idée de la palette de l’auteur, obtenue en considérant ses autres oeuvres. Si l’on peut en faire une statistique raisonnable, on pourra ainsi définir un nuage « de référence », constitué de N points dans le même espace de couleurs. Une technique raisonnable de rehaussement des couleurs consiste alors à effectuer le transport optimal, dans l’espace des couleurs, du nuage de points fourni par l’image défraîchie vers le nuage de points de référence. On déplacera alors en conséquence les valeurs des couleurs de chaque pixel de l’image défraîchie.
Notons que dans cet exemple, c’est bien grâce à la formulation continue que le problème a pu être correctement posé, ceci indépendamment du fait que le calcul numérique est effectué sur un nombre fini de points qui constituent l’image.
Une technique similaire permet d’« effacer » certains éléments d’une photographie.
 |
 |
| Pour faire le portrait d’un oiseau… À gauche, la photo originale, à droite, l’image modifiée. |
|
Ici, on a pu retirer la partie indésirable de la photo en calculant la distance entre les points de l’image et un nuage de points de référence défini à partir de ce qu’il est le plus probable d’y trouver. Dans cette image, il est plus probable de trouver des points correspondant à la texture du perroquet ou du fond que de la grille. L’image modifiée, où la grille est effacée, est donc plus proche de ce qu’il est probable de trouver que l’image de départ, avec la grille. Bien entendu, si la grille avait couvert une plus grande partie de l’image, la méthode aurait pu enlever le perroquet et garder la grille !
Une autre application… aux mathématiques elles-mêmes !
Comme souvent en mathématiques, un problème de « mathématiques appliquées » devient applicable aux mathématiques… « pures ». C’était déjà le cas du travail de Monge, qui, parti d’un problème de génie civil, en arrive à la théorie des enveloppes et des surfaces développables. Dans les années 1990, le théorème décrit dans le paragraphe précédent devient un outil de démonstration puissant et élégant pour démontrer de nombreuses « inégalités » de la géométrie et de l’analyse fonctionnelle.
Le cas le plus simple à décrire est la fameuse « inégalité isopérimétrique », solution du problème de Didon déjà mentionné par Virgile, qui peut s’énoncer ainsi : de toutes les courbes fermées de longueur donnée, celle qui entoure l’aire la plus grande est le cercle.
Ce problème peut être transposé dans l’espace. Étant donné un volume V délimité par une surface fermée d’aire S, on cherche le rapport entre le volume et la surface, et quelle est la surface minimale possible pour un volume donné ou, ce qui revient au même, le volume maximal pour une surface donnée.
On peut montrer l’inégalité :
36πV2 ≤ S3
et que cette inégalité devient une égalité si et seulement si la surface est sphérique. On montre ainsi que la sphère est bien le volume maximal correspondant à une surface donnée.
Parmi différentes démonstrations possibles, on peut le démontrer par la théorie du transport optimal !
On considère les fonctions de densité uniforme et d’intégrale 1, d’une part sur le domaine de volume V, d’autre part sur une boule de rayon 1, donc de volume B = 4π/3. Cela induit l’existence d’un potentiel Φ permettant le transport de la première vers la seconde, solution de l’équation de Monge-Ampère en tout point x du domaine de volume V :
1/V = det(I + D2Φ(x)) 1/B
À partir de là, une inégalité élémentaire de l’analyse (affirmant que la moyenne géométrique d’une suite de nombres réels positifs est toujours supérieure à sa moyenne harmonique) suffit à démontrer l’inégalité isopérimétrique dont il est question ici.
Une méthode similaire est bien sûr utilisée pour réaliser la démonstration d’inégalités non démontrées auparavant.
Pour conclure…
La voici donc bouclée, cette boucle de deux siècles. Une boucle où mathématiques pures et appliquées se répondent, où l’informatique théorique permet de mieux comprendre ce qui peut se calculer efficacement. Et surtout, où c’est en « changeant de point de vue » (ici, en passant d’un problème discret à un problème continu, profitant de la dualité des deux approches) qu’un problème compliqué peut livrer une solution pertinente et inattendue. Pourquoi encore opposer recherche théorique et appliquée, quand manier une brouette permet à un mathématicien de faire émerger une nouvelle idée ?
Newsletter
Le responsable de ce traitement est Inria. En saisissant votre adresse mail, vous consentez à recevoir chaque mois une sélection d'articles et à ce que vos données soient collectées et stockées comme décrit dans notre politique de confidentialité
Niveau de lecture
Aidez-nous à évaluer le niveau de lecture de ce document.
Votre choix a été pris en compte. Merci d'avoir estimé le niveau de ce document !

Yann Brenier